Bienvenue,
Historique des Actions
Baccalauréat 2021 - Mathématiques Spécialité
Session 2021 - Métropole
💡 Conseil : Ouvrez le PDF en plein écran pour une meilleure expérience de navigation
📄 Sujet officiel du Baccalauréat 2021 - Mathématiques Spécialité
Correction détaillée
Exercice 1
Partie I - Probabilités
Question 1 : Arbre pondéré
On obtient l'arbre pondéré suivant :
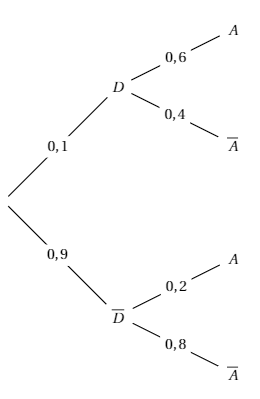
Les probabilités sont :
- $P(D) = 0,1$ (probabilité que le dossier soit sélectionné)
- $P(\overline{D}) = 0,9$ (probabilité que le dossier ne soit pas sélectionné)
- $P_D(A) = 0,6$ (probabilité d'être admis sachant que le dossier est sélectionné)
- $P_D(\overline{A}) = 0,4$
- $P_{\overline{D}}(A) = 0,2$ (probabilité d'être admis sachant que le dossier n'est pas sélectionné)
- $P_{\overline{D}}(\overline{A}) = 0,8$
Question 2 : Calcul de probabilité
On veut calculer $P(D \cap A)$.
D'après la formule des probabilités composées :
$$P(D \cap A) = P(D) \times P_D(A)$$
$$P(D \cap A) = 0,1 \times 0,6 = 0,06$$
Réponse : La probabilité que le candidat soit sélectionné sur dossier et admis à l'école est égale à 0,06.
Question 3 : Système complet d'événements
$(D, \overline{D})$ forme un système complet d'événements fini.
D'après la formule des probabilités totales :
$$P(A) = P(D) \times P_D(A) + P(\overline{D}) \times P_{\overline{D}}(A)$$
$$P(A) = 0,06 + 0,9 \times 0,2$$
$$P(A) = 0,06 + 0,18$$
$$P(A) = 0,24$$
Réponse : La probabilité de l'événement A est égale à 0,24.
Question 4 : Probabilité conditionnelle
On veut calculer $P_A(\overline{D})$, c'est-à-dire la probabilité que le dossier du candidat n'ait pas été sélectionné sachant qu'il a été admis à l'école.
D'après la formule de Bayes :
$$P_A(\overline{D}) = \frac{P(\overline{D} \cap A)}{P(A)}$$
Calculons d'abord $P(\overline{D} \cap A)$ :
$$P(\overline{D} \cap A) = P(\overline{D}) \times P_{\overline{D}}(A) = 0,9 \times 0,2 = 0,18$$
Donc :
$$P_A(\overline{D}) = \frac{0,18}{0,24} = 0,75$$
Réponse : La probabilité que le dossier du candidat n'ait pas été sélectionné sachant qu'il a été admis à l'école est égale à 0,75.
Partie II - Loi binomiale
Question 1.a
$X$ suit la loi binomiale de paramètres $n = 7$ et $p = 0,24$.
Question 1.b
On veut calculer $P(X = 1)$.
$$P(X = 1) = \binom{7}{1} \times 0,24^1 \times (1-0,24)^{7-1}$$
$$P(X = 1) = 7 \times 0,24 \times 0,76^6$$
$$P(X = 1) \approx 7 \times 0,24 \times 0,1927$$
$$P(X = 1) \approx 0,32$$
Réponse : La probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école est environ égale à 0,32.
Question 1.c
On veut calculer $P(X \geqslant 2)$.
$$P(X \geqslant 2) = 1 - P(X \leqslant 1) = 1 - [P(X = 0) + P(X = 1)]$$
Calculons $P(X = 0)$ :
$$P(X = 0) = \binom{7}{0} \times 0,24^0 \times 0,76^7 = 0,76^7 \approx 0,146$$
Donc :
$$P(X \geqslant 2) = 1 - (0,146 + 0,32) = 1 - 0,466 \approx 0,53$$
Réponse : La probabilité qu'au moins deux des sept candidats tirés au sort soient admis à cette école est environ égale à 0,53.
Question 2.a
La probabilité qu'un candidat ne soit pas admis est égale à $1 - 0,24 = 0,76$.
Les résultats des candidats sont indépendants les uns des autres.
Par conséquent, la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école est égale à $0,76^n$.
Question 2.b
La probabilité qu'au moins un élève de ce lycée soit admis à l'école est $1 - 0,76^n$.
On doit donc déterminer le plus petit entier naturel $n$ tel que :
$$1 - 0,76^n \geqslant 0,99$$
$$\Leftrightarrow -0,76^n \geqslant -0,01$$
$$\Leftrightarrow 0,76^n \leqslant 0,01$$
$$\Leftrightarrow n \ln(0,76) \leqslant \ln(0,01)$$
Car $\ln(0,76) < 0$, on inverse le sens de l'inégalité :
$$\Leftrightarrow n \geqslant \frac{\ln(0,01)}{\ln(0,76)}$$
Calculons :
$$\frac{\ln(0,01)}{\ln(0,76)} \approx \frac{-4,605}{-0,274} \approx 16,8$$
Réponse : Le lycée doit donc présenter au moins 17 candidats dans cette école pour que la probabilité qu'au moins un élève de ce lycée soit admis à l'école soit supérieure ou égale à 0,99.
Exercice 2
Question 1.a
Par croissances comparées :
$$\lim_{x \to +\infty} \frac{e^x}{x} = +\infty$$
Question 1.b
$$\lim_{x \to 0^+} \frac{1}{x} = +\infty \text{ et } \lim_{x \to 0^+} e^x = 1$$
Donc :
$$\lim_{x \to 0^+} f(x) = +\infty$$
L'axe des ordonnées est donc asymptote à la courbe $C_f$.
Question 2
La fonction $f$ est dérivable sur $]0; +\infty[$ en tant que quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s'annule pas.
Pour tout réel $x > 0$, on a :
$$f'(x) = \frac{e^x \times x - e^x \times 1}{x^2} = \frac{e^x(x - 1)}{x^2}$$
Question 3
La fonction exponentielle est strictement positive sur $\mathbb{R}$.
Le signe de $f'(x)$ ne dépend donc que de celui de $x - 1$.
- $x - 1 = 0 \Leftrightarrow x = 1$
- $x - 1 > 0 \Leftrightarrow x > 1$
On obtient donc le tableau de variations suivant :
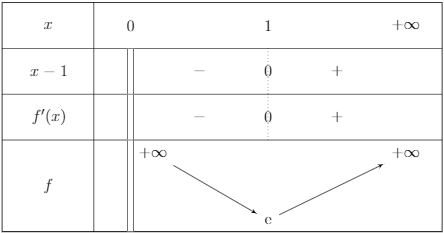
La fonction $f$ admet un minimum en $x = 1$ et ce minimum vaut $f(1) = e$.
Question 4
• Pour tout réel $x > 0$, on a donc $f(x) \geqslant e$.
Ainsi si $m < e$, alors l'équation $f(x) = m$ ne possède pas de solution.
• Soit $m > e$.
La fonction $f$ est continue (car dérivable) strictement décroissante sur l'intervalle $]0; 1]$.
$$\lim_{x \to 0^+} f(x) = +\infty \text{ et } f(1) = e$$
Or $m \in ]e; +\infty[$
D'après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l'équation $f(x) = m$ possède une unique solution sur l'intervalle $]0; 1]$.
La fonction $f$ est continue (car dérivable) strictement croissante sur l'intervalle $]1; +\infty[$.
$$\lim_{x \to +\infty} f(x) = +\infty \text{ et } f(1) = e$$
Or $m \in ]e; +\infty[$
D'après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l'équation $f(x) = m$ possède une unique solution sur l'intervalle $]1; +\infty[$.
Par conséquent, l'équation $f(x) = m$ possède exactement deux solutions sur $]0; +\infty[$.
• Si $m = e$, la fonction $f$ atteint une seule fois son minimum en 1 et celui-ci vaut $e$.
L'équation $f(x) = m$ possède alors une unique solution sur $]0; +\infty[$.
Question 5.a
Le coefficient directeur de la droite $\Delta$ est $-1$.
Deux droites non parallèles à l'axe des ordonnées sont parallèles si, et seulement si, leur coefficients directeurs sont égaux.
Le coefficient directeur d'une tangente à la courbe $C_f$ au point d'abscisse $a$ est $f'(a)$.
Ainsi $a$ est solution, dans $]0; +\infty[$, de l'équation :
$$f'(a) = -1$$
$$\Leftrightarrow \frac{e^a(a-1)}{a^2} = -1$$
$$\Leftrightarrow e^a(a-1) = -a^2$$
$$\Leftrightarrow e^a(a-1) + a^2 = 0$$
Question 5.b
La fonction $g$ est dérivable sur $[0; +\infty[$ d'après l'énoncé.
Pour tout réel $x \geqslant 0$, on a :
$$g'(x) = e^x(x-1) + e^x + 2x$$
$$= xe^x + 2x$$
$$= x(e^x + 2)$$
La fonction exponentielle est strictement positive sur $\mathbb{R}$, donc $e^x + 2 > 0$ sur $\mathbb{R}$.
De plus sur $[0; +\infty[$, on a $x \geqslant 0$ et ne s'annule qu'en 0.
Par conséquent, $g'(x) \geqslant 0$ et $g'(x)$ ne s'annule qu'en 0.
On obtient ainsi le tableau de variations suivant :
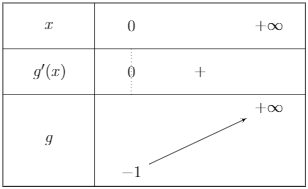
Calculs des limites :
$$\lim_{x \to +\infty} e^x = +\infty, \quad \lim_{x \to +\infty} x - 1 = +\infty \text{ et } \lim_{x \to +\infty} x^2 = +\infty$$
Donc :
$$\lim_{x \to +\infty} g(x) = +\infty$$
Question 5.c
La fonction $g$ est continue (car dérivable) strictement croissante sur $[0; +\infty[$.
$$g(0) = -1 < 0 \text{ et } \lim_{x \to +\infty} g(x) = +\infty$$
Or $0 \in ]-1; +\infty[$
D'après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l'équation $g(x) = 0$ admet une unique solution sur $[0; +\infty[$.
De plus, $g(0) \neq 0$.
Il existe par conséquent un unique point $A$ en lequel la tangente à $C_f$ est parallèle à la droite $\Delta$.
Exercice 3
Question 1
Le point $K$ appartient à $(SD)$ donc $(DK)$ et $(SD)$ sont coplanaires.
$S$ est le milieu de $[AB]$ donc $[SB]$ est inclus dans $(AB)$, donc $(ABCD)$ et $(AS)$ sont coplanaires.
D'après le théorème des milieux (ou de Thalès), la droite $(LM)$ est parallèle à la droite $(BC)$, elle-même parallèle à la droite $(AD)$. Par conséquent, $(LM)$ et $(AD)$ sont coplanaires.
Réponse : c
Question 2
$K$ est le milieu de $[SD]$. Ses coordonnées sont donc :
$$K\left(0; -\frac{1}{2}; \frac{1}{2}\right)$$
$L$ est le milieu de $[SC]$. Ses coordonnées sont donc :
$$L\left(\frac{1}{2}; 0; \frac{1}{2}\right)$$
Ainsi $N$ milieu de $[KL]$ a pour coordonnées :
$$N\left(\frac{1}{4}; -\frac{1}{4}; \frac{1}{2}\right)$$
Réponse : b
Question 3
Les coordonnées du vecteur $\vec{AS}$ sont :
$$\vec{AS} = \begin{pmatrix} 0-(-1) \\ 0-0 \\ 1-0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$$
Réponse : b
Question 4
Un vecteur directeur de la droite $(AS)$ est $\vec{AS} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$.
On exclut donc les propositions a, e et d, dont un vecteur directeur a pour coordonnées :
$$\begin{pmatrix} -1 \\ 1 \\ -1 \end{pmatrix}$$
En prenant $t = 0$ dans les propositions c, on retrouve les coordonnées du point $S$ et en prenant $t = -1$, on retrouve les coordonnées du point $A$.
Réponse : c
Question 5
Si on remplace $x$, $y$ et $z$ par les coordonnées des points $S$, $C$ et $B$, on constate que seule l'équation :
$$x + y + z - 1 = 0$$
convient.
Réponse : b
Exercice A
Question 1
On a :
$$u_1 = \frac{3}{4} \times 1 + 0 + 1 = \frac{7}{4}$$
$$u_2 = \frac{3}{4} \times \frac{7}{4} + \frac{1}{4} + 1 = \frac{21}{16} + \frac{4}{16} + \frac{16}{16} = \frac{41}{16}$$
Question 2.a
On a pu écrire : $3/4 \times B2 + 1/4 + A2 + 1$
Question 2.b
Il semblerait que la suite $(u_n)$ soit strictement croissante.
Question 3.a - Initialisation
Si $n = 0$ alors $u_0 = 1$ et $0 < u_0 \leqslant 0 + 1$
La propriété est donc vraie au rang 0.
Hérédité : Soit $n \in \mathbb{N}$. On suppose la propriété vraie au rang $n$ :
$$n < u_n \leqslant n + 1$$
Montrons qu'elle est vraie au rang $n + 1$ :
$$n < u_n \leqslant n + 1$$
$$\Leftrightarrow \frac{3}{4}n < \frac{3}{4}u_n \leqslant \frac{3}{4}n + \frac{3}{4}$$
$$\Leftrightarrow \frac{3}{4}n + \frac{1}{4}n < \frac{3}{4}u_n + \frac{1}{4}n \leqslant \frac{3}{4}n + \frac{1}{4}n + \frac{3}{4}$$
$$\Leftrightarrow n < \frac{3}{4}u_n + \frac{1}{4}n + \frac{3}{4} \leqslant n + \frac{3}{4}$$
$$\Leftrightarrow n + 1 < \frac{3}{4}u_n + \frac{1}{4}n + \frac{3}{4} + 1 \leqslant n + 1 + \frac{3}{4}$$
Or $n + 2 > n + 1 + \frac{3}{4}$
Ainsi $n + 1 < u_{n+1} \leqslant n + 2$
La propriété est vraie au rang $n + 1$.
Conclusion : La propriété est vraie au rang 0 et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $n < u_n \leqslant n + 1$.
$$\lim_{n \to +\infty} n = +\infty \text{ et, pour tout } n \in \mathbb{N}, \text{ on a } u_n > n$$
D'après le théorème de comparaison :
$$\lim_{n \to +\infty} u_n = +\infty$$
Question 3.b
Pour tout $n \in \mathbb{N}$, on a :
$$u_{n+1} - u_n = \frac{3}{4}u_n + \frac{1}{4}n + 1 - u_n$$
$$= -\frac{1}{4}u_n + \frac{1}{4}n + 1$$
$$= \frac{1}{4}(n - u_n) + 1$$
$$\geqslant \frac{1}{4}(n - (n+1)) + 1$$
$$\geqslant -\frac{1}{4} + 1$$
$$\geqslant \frac{3}{4} > 0$$
La suite $(u_n)$ est donc strictement croissante.
Question 3.c
Pour tout $n \in \mathbb{N}^*$, on a $n \leqslant u_n \leqslant n + 1$ donc $1 \leqslant \frac{u_n}{n} \leqslant 1 + \frac{1}{n}$.
Or :
$$\lim_{n \to +\infty} 1 + \frac{1}{n} = 1$$
D'après le théorème des gendarmes :
$$\lim_{n \to +\infty} \frac{u_n}{n} = 1$$
Question 4.a
Pour tout $n \in \mathbb{N}$, on a :
$$v_{n+1} = u_{n+1} - (n+1)$$
$$= \frac{3}{4}u_n + \frac{1}{4}n + 1 - n - 1$$
$$= \frac{3}{4}u_n - \frac{3}{4}n$$
$$= \frac{3}{4}(u_n - n)$$
$$= \frac{3}{4}v_n$$
La suite $(v_n)$ est donc géométrique de raison $\frac{3}{4}$ et de premier terme $v_0 = u_0 - 0 = 1$.
Question 4.b
Pour tout $n \in \mathbb{N}$, on a donc :
$$v_n = \left(\frac{3}{4}\right)^n$$
Ainsi :
$$u_n = v_n + n = \left(\frac{3}{4}\right)^n + n$$
Exercice B
Question 1.a
Par croissances comparées :
$$\lim_{x \to +\infty} \frac{4}{x} = 0, \quad \lim_{x \to +\infty} \frac{3}{x^2} = 0 \text{ et par croissances comparées } \lim_{x \to +\infty} \frac{\ln(x)}{x} = 0$$
Ainsi :
$$\lim_{x \to +\infty} f(x) = +\infty$$
Question 2
Pour tout réel $x > 0$, on a :
$$f(x) = 1 - \frac{4}{x} + \frac{3}{x^2} = \frac{x^2 - 4x + 3}{x^2}$$
Question 3.a
Le signe de $f'(x)$ ne dépend que de celui de $x^2 - 4x + 3$.
$$\Delta = 16 - 12 = 4 > 0$$
Le polynôme du second degré possède donc deux racines :
$$x_1 = \frac{4-2}{2} = 1 \text{ et } x_2 = \frac{4+2}{2} = 3$$
Le coefficient principal est $a = 1 > 0$.
On obtient donc le tableau de variations suivant :
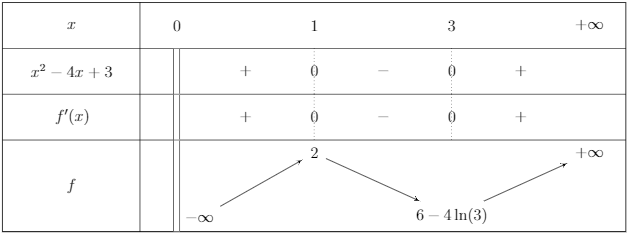
Calcul des extremums :
$$f(1) = 1 - 4 + 3 = 0$$
$$f(3) = 1 - \frac{4}{3} + \frac{3}{9} = 1 - \frac{4}{3} + \frac{1}{3} = 0$$
Question 3.b
On a $6 - 4\ln(3) \approx 1,61$ et $\frac{5}{3} \approx 1,67$.
Ainsi, par lecture du tableau de variations, l'équation $f(x) = \frac{5}{3}$ possède exactement 3 solutions (une dans chaque intervalle du tableau).
Question 4
La fonction $f'$ est dérivable sur $]0; +\infty[$ en tant que quotient de fonctions dérivables sur $]0; +\infty[$ dont le dénominateur ne s'annule pas.
On reprend l'expression de $f'(x) = 1 - \frac{4}{x} + \frac{3}{x^2}$.
Par conséquent, pour tout réel $x > 0$, on a :
$$f''(x) = \frac{4}{x^2} - \frac{6}{x^3} = \frac{4x - 6}{x^3}$$
Sur $]0; +\infty[$, on a $x^3 > 0$ donc $f''(x)$ est du signe de $4x - 6$ sur $]0; +\infty[$.
$$4x - 6 = 0 \Leftrightarrow x = \frac{3}{2}$$
$$4x - 6 > 0 \Leftrightarrow x > \frac{3}{2}$$
La fonction $f$ est donc concave sur $\left]0; \frac{3}{2}\right]$ et convexe sur $\left[\frac{3}{2}; +\infty\right[$.
La fonction $f$ ne change qu'une seule fois de convexité sur $]0; +\infty[$. La courbe $C$ possède donc un unique point d'inflexion d'abscisse $\frac{3}{2}$ et d'ordonnées :
$$f\left(\frac{3}{2}\right) = \frac{3}{2} - 4\ln\left(\frac{3}{2}\right) = \frac{3}{2} - 4\ln(3) + 4\ln(2)$$