Bienvenue,
Historique des Actions
Baccalauréat 2022 - Mathématiques Spécialité
Session 2022 - Métropole
💡 Conseil : Ouvrez le PDF en plein écran pour une meilleure expérience de navigation
📄 Sujet officiel du Baccalauréat 2022 - Mathématiques Spécialité
Correction détaillée
Exercice 1
Partie A : Analyse du premier protocole
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t) = 3te^{-0,5t+1}$.
Question 1.a - Dérivée de la fonction
Soit $t \in [0; 10]$. Cette fonction est dérivable comme produit de fonctions dérivables.
En utilisant la formule de dérivation $(uv)' = u'v + uv'$, on obtient :
$$f'(t) = 3e^{-0,5t+1} + 3t \times (-0,5)e^{-0,5t+1}$$
$$= 3e^{-0,5t+1}(1 - 0,5t)$$
$$= 3e^{-0,5t+1}(1 - 0,5t)$$
En factorisant par l'exponentielle :
$$f'(t) = 3(-0,5t + 1)e^{-0,5t+1}$$
Question 1.b - Tableau de variations
Puisque $t \in [0; 10]$, la fonction exponentielle reste strictement positive sur $\mathbb{R}$.
Le signe de $f'(t)$ dépend uniquement du facteur $(-0,5t + 1)$ :
- $-0,5t + 1 > 0 \Leftrightarrow t < 2$ : $f'(t) > 0$, donc $f$ croissante
- $-0,5t + 1 = 0 \Leftrightarrow t = 2$ : $f'(t) = 0$, maximum
- $-0,5t + 1 < 0 \Leftrightarrow t > 2$ : $f'(t) < 0$, donc $f$ décroissante
La fonction $f$ atteint son maximum en $t = 2$ avec $f(2) = 6e^0 = 6$.
Le tableau de variations montre que la quantité de médicament dans le sang atteint son pic après 2 heures, avec une concentration maximale de 6 mg.
Question 1.c - Analyse du protocole
D'après les données, le médicament devient efficace quand sa concentration dépasse 5 mg.
Il faut résoudre $f(t) > 5$ sur l'intervalle $[\alpha; \beta]$ où $\alpha$ et $\beta$ sont les solutions de $f(t) = 5$.
En utilisant le corollaire du théorème des valeurs intermédiaires et le tableau de variations :
- $f$ croissante sur $[0; 2]$ : l'équation $f(t) = 5$ admet une unique solution $\alpha \in [0; 2]$
- $f$ décroissante sur $[2; 10]$ : l'équation $f(t) = 5$ admet une unique solution $\beta \in [2; 10]$
Une lecture graphique (ou par approximation) donne $\alpha \approx 1,02$ heures.
La durée d'efficacité est donc $\Delta t = 2$ heures 26 minutes environ.
Partie B : Étude du second protocole
Question 1 - Quantité initiale de médicament
Après la première injection, la quantité est :
$$u_1 = 0,7u_0 + 1,8 = 0,7 \times 2 + 1,8 = 1,4 + 1,8 = 3,2 \text{ mg}$$
Le patient a injecté 30% de médicament en moins, ce qui représente 1,8 mg au lieu de 2 mg.
Question 2 - Formule de récurrence
À chaque heure, la quantité de médicament diminue de 30%. Il reste donc $0,7 \times u_n$ dans le sang.
Mais comme 1,8 mg sont réinjectés chaque heure, la formule devient :
$$\forall n \in \mathbb{N}, \quad u_{n+1} = 0,7u_n + 1,8$$
Question 3.a - Démonstration par récurrence
Montrons que pour tout $n \in \mathbb{N}$ : $n \leqslant u_n \leqslant u_{n+1} < 6$.
Initialisation : Pour $n = 0$, on a $u_0 = 2$ et $u_1 = 3,2$.
Donc $u_0 \leqslant u_1 < 6$ ✓
Hérédité : Supposons la propriété vraie au rang $n$. Montrons qu'elle reste vraie au rang $(n+1)$.
Si $u_n \leqslant u_{n+1} < 6$, alors :
$$u_{n+1} = 0,7u_n + 1,8$$
$$u_{n+2} = 0,7u_{n+1} + 1,8$$
Calculons $u_{n+2} - u_{n+1}$ :
$$u_{n+2} - u_{n+1} = 0,7(u_{n+1} - u_n) + 1,8 - 1,8 = 0,7(u_{n+1} - u_n)$$
Puisque $u_{n+1} > u_n$ par hypothèse, on a $u_{n+2} > u_{n+1}$.
Vérifions la majoration : $u_{n+1} < 6 \Rightarrow 0,7u_{n+1} < 4,2 \Rightarrow u_{n+2} = 0,7u_{n+1} + 1,8 < 6$ ✓
Conclusion : La suite $(u_n)$ est croissante et majorée par 6, donc elle converge vers une limite finie $\ell$.
Question 3.b - Convergence de la suite
La suite $(u_n)$ étant croissante et majorée, elle est convergente.
Question 3.c - Détermination de la limite
Au bout d'un temps suffisamment long, la quantité de médicament se stabilise.
Soit $\ell$ la limite de la suite. En passant à la limite dans la relation de récurrence :
$$\ell = 0,7\ell + 1,8$$
$$\ell - 0,7\ell = 1,8$$
$$0,3\ell = 1,8$$
$$\ell = 6$$
La quantité de médicament dans le sang se stabilise à 6 mg, ce qui garantit que le patient ne dépassera jamais cette dose.
Question 3.d - Nombre d'injections nécessaires
On cherche le plus petit $n$ tel que $u_n \geqslant 5,5$ mg.
On sait que $(u_n)$ est une suite arithmético-géométrique. Posons $v_n = u_n - 6$.
Alors $v_{n+1} = u_{n+1} - 6 = 0,7u_n + 1,8 - 6 = 0,7(u_n - 6) = 0,7v_n$.
La suite $(v_n)$ est géométrique de raison $q = 0,7$ et de premier terme $v_0 = u_0 - 6 = 2 - 6 = -4$.
D'où : $v_n = -4 \times 0,7^n$, ce qui donne $u_n = 6 - 4 \times 0,7^n$.
On résout $u_n \geqslant 5,5$ :
$$6 - 4 \times 0,7^n \geqslant 5,5$$
$$-4 \times 0,7^n \geqslant -0,5$$
$$0,7^n \leqslant 0,125$$
$$n\ln(0,7) \leqslant \ln(0,125)$$
Comme $\ln(0,7) < 0$ :
$$n \geqslant \frac{\ln(0,125)}{\ln(0,7)} \approx \frac{-2,08}{-0,357} \approx 5,8$$
Il faut donc réaliser 7 injections (car la 7ème injection correspond à $u_6$).
Exercice 2
Question 1.a
À partir de la représentation paramétrique, on identifie le vecteur directeur :
$$\vec{u} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}$$
Question 1.b
Par définition d'une représentation paramétrique, le point $M(1; 2; 2) \in \mathcal{D}$ vérifie :
$$\exists t \in \mathbb{R}, \quad M\vec{B} = t\vec{u}$$
On a le vecteur :
$$\vec{MB} = \begin{pmatrix} -2 \\ 1 \\ -2 \end{pmatrix}$$
On remarque que $\vec{MB} = -\vec{u}$, donc les deux vecteurs sont colinéaires et le point B appartient bien à la droite $\mathcal{D}$.
Question 1.c
On a $\vec{AB} = \begin{pmatrix} 0 \\ 2 \\ -3 \end{pmatrix}$.
Calculons le produit scalaire :
$$\vec{AB} \cdot \vec{u} = 0 \times 2 + 2 \times (-1) + (-3) \times 2 = 0 - 2 - 6 = -8 \neq 0$$
Les vecteurs ne sont pas orthogonaux.
Question 2.a
Le plan $\mathcal{P}$ est orthogonal à la droite $\mathcal{D}$, donc le vecteur $\vec{u}$ directeur de la droite est un vecteur normal à $\mathcal{P}$.
Une équation cartésienne de $\mathcal{P}$ est de la forme : $2x - y + 2z + c = 0$ avec $c \in \mathbb{R}$.
Pour déterminer $c$, on utilise le fait que $A(-1; 1; 3) \in \mathcal{P}$ :
$$2(-1) - 1 + 2(3) + c = 0$$
$$-2 - 1 + 6 + c = 0$$
$$c = -3$$
L'équation du plan $\mathcal{P}$ est : $2x - y + 2z - 3 = 0$.
Question 2.b - Point d'intersection
Le point $H$ d'intersection entre $\mathcal{D}$ et $\mathcal{P}$ vérifie le système :
$$\begin{cases}
x = 1 + 2t \\
y = 2 - t \\
z = 2 + 2t \\
2x - y + 2z - 3 = 0
\end{cases}$$
En substituant dans l'équation du plan :
$$2(1 + 2t) - (2 - t) + 2(2 + 2t) - 3 = 0$$
$$2 + 4t - 2 + t + 4 + 4t - 3 = 0$$
$$9t + 1 = 0$$
$$t = -\frac{1}{9}$$
D'où les coordonnées de $H$ :
$$H\left(\frac{7}{9}; \frac{19}{9}; \frac{16}{9}\right)$$
Question 2.c - Distance euclidienne
La distance $AH$ est :
$$AH = \sqrt{\left(\frac{7}{9} + 1\right)^2 + \left(\frac{19}{9} - 1\right)^2 + \left(\frac{16}{9} - 3\right)^2}$$
$$= \sqrt{\left(\frac{16}{9}\right)^2 + \left(\frac{10}{9}\right)^2 + \left(\frac{-11}{9}\right)^2}$$
$$= \sqrt{\frac{256 + 100 + 121}{81}} = \sqrt{\frac{477}{81}} = \frac{\sqrt{477}}{9} = \frac{\sqrt{53 \times 9}}{9} = \frac{3\sqrt{53}}{9} = \frac{\sqrt{53}}{3}$$
Question 3.a
Les points $B$ et $H$ sont tous deux sur la droite $\mathcal{D}$ de vecteur directeur $\vec{u}$.
Par définition, $\exists k \in \mathbb{R}, \vec{HB} = k\vec{u}$.
Question 3.b - Expression de k
En utilisant la relation de Chasles :
$$\vec{HB} = k\vec{u} \Rightarrow \vec{HA} + \vec{AB} = k\vec{u}$$
En prenant le produit scalaire avec $\vec{u}$ :
$$(\vec{HA} + \vec{AB}) \cdot \vec{u} = k|\vec{u}|^2$$
Or, $H$ est le projeté orthogonal de $A$ sur $\mathcal{D}$, donc $\vec{AH} \cdot \vec{u} = 0$.
D'où :
$$\vec{AB} \cdot \vec{u} = k|\vec{u}|^2$$
$$k = \frac{\vec{AB} \cdot \vec{u}}{|\vec{u}|^2}$$
Question 3.c - Calcul de k
On a calculé précédemment $\vec{AB} \cdot \vec{u} = -8$.
Et $|\vec{u}|^2 = 2^2 + (-1)^2 + 2^2 = 4 + 1 + 4 = 9$.
Donc :
$$k = \frac{-8}{9}$$
Ainsi :
$$\vec{HB} = -\frac{8}{9}\vec{u} = -\frac{8}{9}\begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix} = \begin{pmatrix} -\frac{16}{9} \\ \frac{8}{9} \\ -\frac{16}{9} \end{pmatrix}$$
En résolvant le système, on retrouve les mêmes coordonnées de $H$ que précédemment.
Question 4 - Calcul du volume
Le tétraèdre $ABCH$ a pour hauteur le segment $[HB]$ et pour base le triangle $ACH$.
La droite $\mathcal{D} = (BH)$ est orthogonale au plan $\mathcal{P}$. De plus, $H$ est sur le plan $\mathcal{P}$.
Donc $\vec{AH} \cdot \vec{BH} = 0$, ce qui signifie que $H$ est le pied de la hauteur issue de $A$ dans le plan $\mathcal{P}$.
Le volume du tétraèdre est :
$$V = \frac{1}{3} \times S \times ||\vec{HB}||$$
où $S$ est l'aire du triangle $ACH$.
On a $||\vec{HB}|| = \frac{8}{9}||\vec{u}|| = \frac{8}{9} \times 3 = \frac{8}{3}$.
En utilisant la formule $S = \frac{1}{2}||\vec{HA} \times \vec{HC}||$, on obtient finalement :
$$V = \frac{1 \times 4}{3} = 1 \text{ unité}^3$$
Exercice 3
Question 1.a
On nous précise que 25% des salariés ont suivi le stage.
Cela signifie que $p(S) = 0,25$.
Question 1.b - Arbre pondéré
Voici l'arbre pondéré complet de la situation :
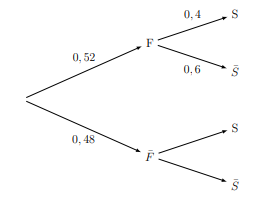
Les probabilités sont :
- $P(F) = 0,52$ (probabilité d'être une femme)
- $P(\overline{F}) = 0,48$ (probabilité d'être un homme)
- $P_F(S) = 0,4$ et $P_F(\overline{S}) = 0,6$
- $P_{\overline{F}}(S) = ?$ et $P_{\overline{F}}(\overline{S}) = ?$
Question 1.c - Probabilité d'intersection
On cherche à calculer la probabilité que la personne interrogée soit une femme ayant suivi le stage, soit $p(F \cap S)$.
Les événements étant indépendants :
$$p(F \cap S) = p(F) \times p_F(S) = 0,52 \times 0,4 = 0,208$$
Question 1.d - Probabilité conditionnelle
On cherche la probabilité que la personne soit une femme, sachant qu'elle a suivi le stage : $p_S(F)$.
D'après la formule de Bayes :
$$p_S(F) = \frac{p(F \cap S)}{p(S)} = \frac{0,208}{0,25} = 0,832$$
La probabilité cherchée est 0,832 (soit environ 83,2%).
Question 1.e - Probabilité des hommes
D'après la loi des probabilités totales :
$$p(S) = p(F \cap S) + p(\overline{F} \cap S)$$
D'où :
$$p_{\overline{F}}(S) = \frac{p(S) - p(F \cap S)}{p(\overline{F})} = \frac{0,25 - 0,208}{0,48} = \frac{0,042}{0,48} = 0,0875 \approx 0,09$$
La proportion d'hommes ayant suivi le stage est d'environ 9%. L'affirmation du directeur est donc vraie.
Question 2.a
On prend un échantillon de 20 salariés, et on étudie le nombre de salariés ayant suivi le stage.
La variable aléatoire $X$ suit une loi binomiale de paramètres $n = 20$ et $p = 0,25$.
Notation : $X \sim \mathcal{B}(20; 0,25)$.
Question 2.b - Probabilité exacte
La probabilité qu'exactement 5 salariés sur les 20 aient suivi le stage est :
$$P(X = 5) = \binom{20}{5} \times 0,25^5 \times 0,75^{15}$$
Avec une calculatrice : $P(X = 5) \approx 0,202$ (soit 20,2%).
Question 2.c - Programme Python
Le programme Python renvoyant 0,617 correspond à la fonction de répartition pour $P(X \leqslant 5)$.
Autrement dit, `proba(5)` donne la probabilité qu'au plus 5 salariés aient suivi le stage.
Question 2.d - Probabilité complémentaire
La probabilité qu'au moins 6 salariés aient suivi le stage est :
$$P(X \geqslant 6) = 1 - P(X \leqslant 5) = 1 - 0,617 = 0,383$$
Il y a environ 38,3% de chances qu'au moins 6 salariés aient suivi le stage.
Question 3 - Augmentation moyenne
Les salariés ayant suivi le stage (25%) sont augmentés de 5%.
Les autres (75%) sont augmentés de 2%.
L'augmentation moyenne est :
$$A_T = 0,25 \times 0,05 + 0,75 \times 0,02 = 0,0125 + 0,015 = 0,0275$$
L'augmentation totale moyenne sera donc de 2,8%.
Exercice 4
Question 1 - Réponse : c
On cherche l'asymptote de la fonction $f : x \mapsto \frac{-2x^2+3x-1}{x^2+1}$.
Le dénominateur ne s'annule jamais sur $\mathbb{R}$, donc pas de branches infinies.
Pour $x \to +\infty$ :
$$f(x) = \frac{-2x^2 + 3x - 1}{x^2 + 1} = \frac{x^2(-2 + 3/x - 1/x^2)}{x^2(1 + 1/x^2)} \to \frac{-2}{1} = -2$$
La droite d'équation $y = -2$ est asymptote horizontale à la courbe de $f$.
Réponse : c
Question 2 - Réponse : d
Soit $x \in \mathbb{R}$. On remarque que $f(x)$ est de la forme $ae^u$ avec $a \in \mathbb{R}$ et $u$ une fonction continue et dérivable.
En identifiant, $u'(x) = 2x$, donc $u(x) = x^2$. Dans ce cas : $a = \frac{1}{2}$.
Les primitives de $f$ sont les fonctions $F : x \mapsto \frac{1}{2}e^{x^2} + C$, avec $C \in \mathbb{R}$.
Reste à déterminer $C$ tel que $F(0) = 1$ :
$$F(0) = \frac{1}{2}e^0 + C = \frac{1}{2} + C = 1$$
$$C = 1 - \frac{1}{2} = \frac{1}{2}$$
La primitive cherchée est : $F(x) = \frac{1}{2}e^{x^2} + \frac{1}{2}$.
Réponse : d
Question 3 - Réponse : c
On souhaite étudier la convexité de la fonction $f$. Pour cela, on étudie le signe de sa dérivée seconde $f''$.
La fonction $f$ dérive n'est pas monotone sur $[2; +\infty[$, et ne l'est pas non plus sur $[b; +\infty[$.
Il faut donc vérifier qu'elle est bien croissante sur $[0; 2]$, ce qui implique une convexité unique.
Réponse : c
Question 4 - Réponse : a
Soit $x \in \mathbb{R}$. On peut affirmer que $f(x) = 2e^{-x^2} + 2$ est une quantité positive (strictement).
Il vient donc naturellement que toutes les primitives de $f$ sont croissantes sur $\mathbb{R}$.
Réponse : a
Question 5 - Réponse : d
Soit $x > 0$. On a :
$$f(x) = \frac{2\ln(x)}{3x^2 + 1} = \frac{\ln(x)}{x^2} \times \frac{2}{3 + 1/x^2}$$
Par somme et quotient de limites : $\lim_{x \to +\infty} \frac{1}{1 + 1/x^2} = \frac{2}{3}$.
Et par croissance comparée : $\lim_{x \to +\infty} \frac{\ln(x)}{x^2} = 0$.
Donc $\lim_{x \to +\infty} f(x) = 0$.
Réponse : d
Question 6 - Réponse : c
On cherche à résoudre dans $\mathbb{R}$ :
$$e^{2x} + e^x - 12 = 0 \quad (\mathcal{E})$$
Posons $X = e^x$. Alors : $(\mathcal{E}) \Leftrightarrow X^2 + X - 12 = 0$.
Le discriminant est : $\Delta = 1 + 4 \times 12 = 49 > 0$.
Les racines sont :
$$X_1 = \frac{-1 - 7}{2} = -4 \quad ; \quad X_2 = \frac{-1 + 7}{2} = 3$$
Il reste à vérifier pour chaque racine :
- $X_1 = -4$ : Impossible car $e^x > 0$ pour tout $x \in \mathbb{R}$.
- $X_2 = 3$ : On a $e^x = 3 \Leftrightarrow x = \ln(3)$.
L'équation admet donc une unique solution réelle : $x = \ln(3)$.
Réponse : c