Bienvenue,
Historique des Actions
Baccalauréat 2023 - Mathématiques Spécialité
Session 2023 - Métropole
💡 Conseil : Ouvrez le PDF en plein écran pour une meilleure expérience de navigation
📄 Sujet officiel du Baccalauréat 2023 - Mathématiques Spécialité
Correction détaillée
Exercice 1
Partie A : Construction de l'arbre pondéré
D'après l'énoncé, on peut établir l'arbre pondéré suivant :
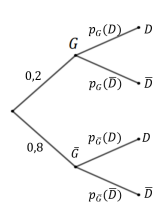
On sait que $p(G \cap D) = 0,002$ et $p(D) = 0,082$.
Question 1 : Calcul de $p_G(D)$
Par définition de la probabilité conditionnelle :
$$p_G(D) = \frac{p(G \cap D)}{p(G)} = \frac{0,2}{20} = 0,01$$
La réponse est B.
Question 2 : Application de la formule des probabilités totales
Puisque $(G, \overline{G})$ constitue une partition complète de l'univers, nous pouvons écrire :
$$p(D) = p(G) \times p_G(D) + p(\overline{G}) \times p_{\overline{G}}(D)$$
Ce qui équivaut à :
$$p(D \cap G) = p(D) - p(D \cap \overline{G}) = 0,082 - 0,002 = 0,08$$
La réponse est B.
Question 3 : Calcul de $p_D(G)$
On cherche à déterminer la probabilité conditionnelle $p_D(G)$.
En utilisant la définition :
$$p_D(G) = \frac{p(G \cap D)}{p(D)} = \frac{0,2}{0,244} \simeq 0,024 \simeq 0,024$$
La réponse est B.
Question 4 : Application de la loi binomiale
On se place dans le cadre d'un schéma de Bernoulli avec $n = 50$ répétitions indépendantes et $p = 0,082$.
Soit $X$ la variable aléatoire comptant le nombre de succès. Alors $X$ suit une loi binomiale $\mathcal{B}(50; 0,082)$.
On cherche $P(X > 2)$.
En utilisant l'événement complémentaire :
$$P(X > 2) = 1 - P(X \leqslant 2) = 1 - P(X = 0) - P(X = 1) - P(X = 2)$$
Calculs détaillés :
- $P(X = 0) = (1 - 0,082)^{50} \times 0,082^0 = 0,918^{50} \approx 50 \times 0,082 \times (1 - 0,082)^{49}$
On obtient finalement :
$$P(X > 2) = 1 - (1 - 0,082)^{50} - 50 \times 0,082 \times (1 - 0,082)^{49} = 0,78888 \simeq 0,789$$
La réponse est B.
Question 5 : Inégalité et détermination de $n$
On souhaite déterminer le plus petit entier $n$ tel que $P(X = 0) > 0,4$ où $X \sim \mathcal{B}(n; 0,082)$.
Nous avons :
$$P(X = 0) = \binom{n}{0} \times 0,082^0 \times (1 - 0,082)^n = (1 - 0,082)^n$$
L'inégalité devient :
$$(1 - 0,082)^n > 0,4 \Leftrightarrow (1 - 0,082)^n > 0,4$$
En appliquant le logarithme népérien (fonction strictement croissante sur $\mathbb{R}_+^*$) :
$$n \log(1 - 0,082) > \log(0,4)$$
Puisque $\log(1 - 0,082) < 0$, on inverse le sens de l'inégalité lors de la division :
$$n < \frac{\log(0,4)}{\log(0,918)} \Leftrightarrow n < 10,7$$
Après calculs, on trouve $n < 10,7$, donc $n \leqslant 10$.
La réponse est C.
Exercice 2
On considère la fonction $f$ définie sur $]0; +\infty[$ par :
$$f(x) = 2x - 2 - \frac{8}{x} - \frac{8\ln(x)}{x}$$
Question 1 : Limites aux bornes du domaine
En $+\infty$ :
Par opérations sur les limites usuelles :
$$\lim_{x \to +\infty} x^2 = +\infty \text{ et } \lim_{x \to +\infty} \ln(x) = +\infty$$
De plus, par croissance comparée :
$$\lim_{x \to +\infty} \frac{\ln(x)}{x} = 0$$
Donc :
$$\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} 2x = +\infty$$
En $0^+$ :
En utilisant les limites classiques :
$$\lim_{x \to 0^+} \frac{8}{x} = +\infty$$
De même, sachant que $\lim_{x \to 0^+} \ln(x) = -\infty$ et $\lim_{x \to 0^+} \frac{1}{x} = +\infty$ :
$$\lim_{x \to 0^+} \frac{\ln(x)}{x} = -\infty$$
Par somme, on obtient :
$$\lim_{x \to 0^+} f(x) = +\infty$$
Question 2 : Étude des croissances composées
En factorisant par $x^2$ au dénominateur :
$$\lim_{x \to +\infty} \frac{\ln(x)}{x^2} = 0$$
Par opérations :
$$\lim_{x \to +\infty} f(x) = +\infty \cdot (1 - 8 \times 0) = +\infty$$
Question 3 : Calcul de la dérivée
La fonction $f$ est dérivable sur $]0; +\infty[$ comme somme et quotient de fonctions dérivables.
Pour tout $x \in ]0; +\infty[$ :
$$f'(x) = 2x - 2 - \frac{8}{x^2} - \frac{8}{x} = \frac{2x^2 - 8x - 2(x^2 - 8x)}{x^2} = \frac{2(x^2 - 4)}{x^2}$$
Question 4 : Tableau de signes et variations
Le numérateur $2(x^2 - 4)$ s'annule pour $x = 2$ (on écarte $x = -2$ car hors du domaine).
Tableau de signes :
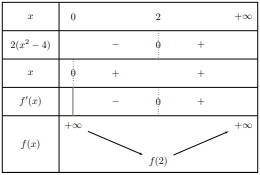
On constate que :
- $f$ est décroissante sur $]0; 2]$
- $f$ possède un minimum en $x = 2$ avec $f(2) = 4 - 8\ln(2) = 4(1 - \ln(4)) \simeq -1,54$
- $f$ est croissante sur $[2; +\infty[$
Question 5 : Analyse du nombre de solutions
D'après le tableau de variations précédent :
- $f$ est continue sur $]0; 2]$ avec $\lim_{x \to 0^+} f(x) = +\infty$ et $f(2) \simeq -1,54$
- Puisque $0 \in ]f(2); +\infty[$, le corollaire du TVI garantit l'existence d'une unique solution $\theta \in ]0; 2]$ à l'équation $f(x) = 0$
Conclusion : L'équation $f(x) = 0$ admet une unique solution sur $]0; 2]$.
Question 6 : Tableau de signes complet
À partir des résultats précédents, on déduit le tableau de signes de $f$ :

- Sur $]0; \alpha[$, $f(x) > 0$
- En $x = \alpha$, $f(\alpha) = 0$
- Sur $]\alpha; \beta[$, $f(x) < 0$
- En $x = \beta$, $f(\beta) = 0$
- Sur $]\beta; +\infty[$, $f(x) > 0$
Question 7 : Translation et nouvelle fonction
Soit $g_k$ la fonction définie par $g_k(x) = f(x) + k$ pour tout $x \in ]0; +\infty[$.
On cherche à déterminer la valeur de $k$ telle que $g_k$ soit positive.
Le tableau de variations de $g_k$ se déduit de celui de $f$ par translation verticale :
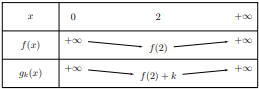
Pour que $g_k$ soit positive, il suffit que son minimum soit positif :
$$f(2) + k \geqslant 0 \Leftrightarrow k \geqslant -f(2)$$
La plus petite valeur de $k$ telle que $g_k$ reste positive est donc $k = -f(2) = 8\ln(2) - 4$.
Exercice 3
Première modélisation
Question 1 : Calcul des premiers termes
On a $u_2 = 0,9 \times 3 + 1,3 = 4$ et $u_3 = 0,9 \times 4 + 1,3 = 4,9$.
Au 2ème mois de la FAQ, la modélisation prévoit 400 questions, et au 3ème mois 490 questions.
Question 2 : Propriété de la suite
Notons que $\forall n \in \mathbb{N}$, la propriété $\mathcal{H}(n)$ est vraie si $0 < 0,9^n \leqslant 0,9^n$.
Cette propriété est vérifiée pour tout $n \in \mathbb{N}$.
Question 3 : Initialisation de la récurrence
Posons $u_1 = -3$ et $u_2 = \frac{100}{9} \times 0,9 = 10$.
Alors $u_1 = 0,9(u_0 - 13) = -3$ et $u_0 = 13 - 10 - 3 = 0$.
Hérédité : Soit $n \in \mathbb{N}$. Supposons que $\mathcal{H}(n)$ est vraie.
On a :
$$u_{n+1} = 0,9u_n + 1,3 = 0,9 \times \left(13 - \frac{100}{9} \times 0,9^{n+1}\right) + 1,3$$
Par récurrence, la propriété est donc démontrée.
Conclusion : On a prouvé que $\forall n \in \mathbb{N}$, $\mathcal{H}(n)$ est vraie.
La propriété est vérifiée par principe de récurrence.
Question 4 : Calcul du rang
On cherche le premier rang $N$ tel que $u_N > p$.
D'après le programme :
$$u_n > 8,5 \Longleftrightarrow 13 - \frac{100}{9} \times 0,9^n > 8,5$$
Résolvons :
$$\frac{100}{9} \times 0,9^n < 4,5 \Leftrightarrow 0,9^n < 0,405$$
En appliquant le logarithme :
$$n \log(0,9) < \log(0,405) \Longleftrightarrow n > \frac{\log(0,405)}{\log(0,9)} \simeq 8,57$$
Le programme renvoie donc $N = 9$.
Une autre modélisation
Question 1 : Calcul initial
On a $v_1 = 9 - 6 = 3,00$ et $v_2 = 9 - 6e^{-0,15} \simeq 4,04$.
Question 2 : Résolution de l'équation
On cherche $n$ tel que $v_n = 8,5$.
$$9 - 6e^{-0,15(n-1)} = 8,5 \Longleftrightarrow e^{-0,15(n-1)} = \frac{0,5}{6} = -0,19(n - 1) = -\ln(12)$$
D'où :
$$n = 1 + \frac{\ln(12)}{0,19} \simeq 15$$
On trouve après calculs $n = 15$.
Comparaison des deux modèles
Question 1 : Analyse comparative
Il s'agit de comparer les questions A.4 et B.2.
La première modélisation dépasse les 850 questions au 9ème mois alors que la deuxième modélisation les atteint seulement au 15ème mois.
La première modélisation aboutit donc à un résultat plus rapide.
Question 2 : Étude des limites
Pour les deux suites $(u_n)$ et $(v_n)$, il faut calculer leurs limites.
Pour la suite géométrique :
$$\lim_{n \to +\infty} u_n = 13 - \frac{100}{9} \times 0 = 13$$
De plus, on sait que $\lim_{n \to +\infty} \exp(-n) = 0$, donc :
$$\lim_{n \to +\infty} v_n = 9 - 6 \times 0 = 9$$
La 1ère modélisation prévoit plus de questions : au maximum 1300 alors que la 2ème modélisation n'en prévoit que 900.
Exercice 4
Question 1 : Calcul de point
On doit calculer :
$$E = \begin{pmatrix} 0 \\ 1 \end{pmatrix} + E \begin{pmatrix} 1 \\ 0 \end{pmatrix} + C \begin{pmatrix} 1 \\ 1 \end{pmatrix}$$
En identifiant les coordonnées, on trouve le point.
Question 2 : Vecteur directeur et représentation paramétrique
Il faut un point appartenant à $(EC)$ ainsi qu'un vecteur directeur de $(EC)$.
On a $\vec{EC} = \begin{pmatrix} 1-0 \\ u-0 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \end{pmatrix}$.
Une représentation paramétrique de $(EC)$ est donc :
$$\begin{cases} x = 0 + t \\ y = 0 + t \\ z = 1 + t \end{cases}, \quad t \in \mathbb{R}$$
Ce qui équivaut à :
$$\begin{cases} x = t \\ y = t \\ z = -1 - t \end{cases}, \quad t \in \mathbb{R}$$
Question 3 : Vecteurs directeurs d'un plan
On calcule :
$$\vec{GB} = \begin{pmatrix} 1-1 \\ 0-1 \\ -1-1 \end{pmatrix} = \begin{pmatrix} 0 \\ -1 \\ -1 \end{pmatrix} \text{ et } \vec{GD} = \begin{pmatrix} 1 \\ 0-1 \\ -1-1 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 0 \end{pmatrix}$$
Ce sont deux vecteurs directeurs du plan (GBD), donc $\vec{EC}$ est un vecteur directeur de la droite $(EC)$.
Vérifions l'orthogonalité :
$$\vec{GB} \cdot \vec{EC} = 1 \times 0 - 1 \times (-1) - 1 \times (-1) = 0$$
De même :
$$\vec{GD} \cdot \vec{EC} = 1 \times (-1) + 0 \times 1 + 1 \times (-1) \times (-1) = 0$$
Ainsi, $\vec{EC}$ est orthogonal à $\vec{GB}$ et $\vec{GD}$, donc (EC) est orthogonal au plan (GBD).
Question 4a : Vecteur normal et équation du plan
Un vecteur normal $\vec{n}$ suffit généralement à caractériser un plan.
Dans notre cas, l'équation cartésienne du plan est de la forme $ax + by + cz + d = 0$ avec $a \in \mathbb{R}$.
Puisque $\vec{EC}$ est normal à (BCG), on peut prendre $\vec{n} = \vec{EC}$.
L'équation cartésienne de (BCG) est donc de la forme $1x + 1y - 1z + d = 0$.
Il reste à déterminer $d$. On sait que $B \in (BCG)$, donc ses coordonnées vérifient l'équation :
$$x_B + y_B - z_B + d = 0 \Longrightarrow 1 + 0 + 0 + d = 0 \Longrightarrow d = -1$$
L'équation du plan est donc : $x + y - z - 1 = 0$.
Question 4b : Intersection de (BDG) et (EC)
L'est l'intersection de (BDG) et de (EC) vérifie le système :
$$\begin{cases} t_B + t_B - z_B - 1 = 0 \\ x_B = t_B \\ y_B = t_B \\ z_B = t - t_B \end{cases}$$
En substituant :
$$t_B + t_B + t_B - 1 = 0 \Longrightarrow 3t_B + t_B = 1 \Longrightarrow t_B = \frac{2}{3}$$
Les coordonnées de I sont donc :
$$I = \begin{pmatrix} \frac{2}{3} \\ \frac{2}{3} \\ \frac{-2}{3} \end{pmatrix}$$
Puis :
$$x_B = t_B \Longrightarrow z_B = t_B \Longrightarrow t_B = \frac{2}{3}$$
Les coordonnées de I sont donc :
$$\begin{pmatrix} \frac{2}{3} \\ \frac{2}{3} \\ \frac{-2}{3} \end{pmatrix}$$
Question 4c : Interprétation géométrique
Un schéma permet de se rendre compte que $d(E; GBD) = |\vec{EI}|$.
Et, Or, $\vec{EI} = \begin{pmatrix} \frac{2}{3} - 0 \\ \frac{2}{3} - 1 \\ \frac{-2}{3} - 1 \end{pmatrix} = \begin{pmatrix} \frac{2}{3} \\ \frac{2}{3} \\ \frac{-2}{3} \end{pmatrix}$.
Donc :
$$EI = \sqrt{\left(\frac{2}{3}\right)^2 + \left(\frac{2}{3}\right)^2 + \left(\frac{2}{3}\right)^2} = \frac{2\sqrt{3}}{3} = \frac{2}{\sqrt{3}}$$
Question 5a : Longueurs et géométrie du triangle
Pour montrer que BDG est équilatéral, il suffit de montrer que ses 3 côtés sont de même longueur.
On calcule donc la norme des vecteurs associés :
$$|\vec{GB}| = \sqrt{0^2 + (-1)^2 + (-1)^2} = \sqrt{2}$$
$$|\vec{GD}| = \sqrt{(-1)^2 + (-1)^2 + 0^2} = \sqrt{2}$$
Il reste à calculer $|\vec{DB}|$.
Calculons :
$$\vec{DB} = \begin{pmatrix} t \\ -1 \end{pmatrix}$$
De norme $|\vec{DB}| = \sqrt{2}$.
Donc BDG est un triangle équilatéral de côté $\sqrt{2}$.
Question 5b : Aire du triangle
Or, BDG est un triangle rectangle en J (grâce aux propriétés sur les triangles équilatéraux).
Donc en appliquant le théorème de Pythagore dans BJG, on trouve :
$$JG^2 + JB^2 = BG^2 \Longrightarrow JG = \sqrt{BG^2 - JB^2} = \sqrt{2 - \frac{1}{2}} = \sqrt{\frac{3}{2}}$$
car $JB = DB/2 = \frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}$.
L'aire du triangle BJG est :
$$\mathcal{A}_{BJG} = \frac{JG \times JB}{2} = \frac{\sqrt{3}}{4} \text{ (motif de l'aire d'un rectangle)}$$
Et donc :
$$\mathcal{A}_{BDG} = \frac{\sqrt{3}}{2}$$
Question 6 : Volume du tétraèdre
Le tétraèdre EGBD a pour base BDG et pour hauteur relative EI.
Donc :
$$\mathcal{V}_{EGBD} = \frac{1}{3} \mathcal{A}_{BDG} \times EI = \frac{1}{3} \times \frac{\sqrt{3}}{2} \times \frac{2}{\sqrt{3}} = \frac{1}{3}$$