Baccalauréat 2024 - Mathématiques Spécialité

Exercice 2

Question 1 : Arbre pondéré

D'après l'énoncé, voici l'arbre pondéré complet :

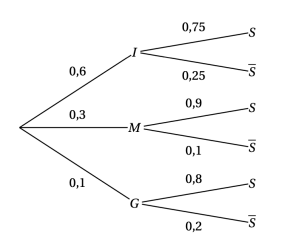
Les probabilités sont :

• $P(I) = 0,6$, $P(M) = 0,3$, $P(G) = 0,1$
• $P(S) = 0,9$, etc.

Question 2 : Probabilité d'achat sur internet et satisfaction

On cherche $P(I \cap S)$.

En utilisant la formule des probabilités composées :
$$P(I \cap S) = P(I) \times P_I(S)$$

D'après l'arbre pondéré :
$$P(I \cap S) = 0,6 \times 0,75 = 0,45$$

La probabilité que le client ait réalisé son achat sur Internet et qu'il soit satisfait du service client est de 0,45.

Question 3 : Formule des probabilités totales

On connaît :
$$P(S) = 0,45 + 0,9 \times 0,3 + 0,8 \times 0,1$$

Calculons :
$$P(S) = 0,45 + 0,27 + 0,08 = 0,8$$

On utilise ici la formule des probabilités totales avec $(I, M, G)$ qui forment un système complet d'événements :
$$P(S) = P(I) \times P_I(S) + P(M) \times P_M(S) + P(G) \times P_G(S)$$

Donc, d'après la formule des probabilités totales :
$$P(S) = 0,8$$

Question 4 : Probabilité conditionnelle

On cherche $P_S(I)$.

En appliquant la formule de Bayes :
$$P_S(I) = \frac{P(I \cap S)}{P(S)} = \frac{0,45}{0,8} = 0,5625 \simeq 0,563 \times 10^{-3} \text{ près}$$

La probabilité que le client ait fait son achat sur Internet sachant qu'il est satisfait du service client est d'environ 0,563.

Question 5 : Loi binomiale

a) Appeler un client pour savoir s'il est satisfait du service client est une épreuve de Bernoulli dont le succès est « le client est satisfait » de probabilité $P(S) = 0,8$.

On répète 30 fois cette épreuve de façon identique et indépendante (on suppose que le choix du client est assimilable à un tirage avec remise). On a donc un schéma de Bernoulli de paramètres $n = 30$ et $p = 0,8$.

La variable aléatoire $X$ qui compte le nombre de succès (le nombre de clients satisfaits sur la journée) suit donc la loi binomiale $\mathcal{B}(30; 0,8)$.

b) On cherche $P(X \geqslant 25)$.

Calculons $P(X \geqslant 25) = 1 - P(X < 25) = 1 - P(X \leqslant 24)$.

D'après la calculatrice, $P(X \geqslant 25) \simeq 0,428$.

La probabilité qu'au moins 25 clients soient satisfaits dans un échantillon de 30 clients contactés sur une même journée est d'environ 0,428.

Question 6 : Détermination de n

Soit $n$ la taille minimale de l'échantillon et $Y$ la variable aléatoire qui, sur ces $n$ clients contactés en une journée, compte le nombre de clients non satisfaits.

Appeler un client pour savoir s'il est satisfait du service client est une épreuve de Bernoulli de paramètres $n$ et $p = 0,2$ (probabilité d'être non satisfait).

La variable aléatoire $Y$ qui compte le nombre de succès (le nombre de clients non satisfaits sur la journée) suit donc la loi binomiale $\mathcal{B}(n; 0,2)$.

On cherche $n$ tel que $P(Y \geqslant 1) > 0,99$.

$$P(Y \geqslant 1) = 1 - P(Y = 0) = 1 - 0,8^n$$

Comme $Y$ suit $\mathcal{B}(n; 0,2)$, on a :
$$P(Y = 0) = \binom{n}{0} \times 0,2^0 \times 0,8^n = 0,8^n$$

On veut donc $1 - 0,8^n > 0,99$, ce qui équivaut à $0,8^n < 0,01$.

En passant au logarithme népérien (qui est une fonction strictement croissante sur $\mathbb{R}_+^*$, les quantités étudiées étant strictement positives) :
$$n \ln(0,8) < \ln(0,01)$$

Comme $\ln(0,8) < 0$, on inverse le sens de l'inégalité lors de la division :
$$n > \frac{\ln(0,01)}{\ln(0,8)} \Leftrightarrow n > \frac{-\ln(0,01)}{-\ln(0,8)}$$

Pour tout $n \in \mathbb{N}$, $1 - 0,8^n \geqslant 0,99 \Leftrightarrow 0,8^n \leqslant 0,01 \Leftrightarrow n \ln(0,8) \leqslant \ln(0,01)$ car la fonction $\ln$ est croissante sur $\mathbb{R}_+^*$.

$$\Leftrightarrow n \geqslant \frac{\ln(0,01)}{\ln(0,8)}$$ car $\ln(0,8) < 0$ car $0 < 0,8 < 1$.

D'après la calculatrice, $\frac{\ln(0,01)}{\ln(0,8)} = 20,64$. Donc, $n$ étant entier, il faut $n \geqslant 21$.

Il faut donc appeler au minimum 21 clients sur une même journée pour que la probabilité qu'au moins l'un d'entre eux ne soit pas satisfait soit supérieure ou égale à 0,99.

Question 7 : Espérance et variance

a) Par linéarité de l'espérance, on a $E(T) = E(T_1 + T_2) = E(T_1) + E(T_2)$.

Donc $E(T) = 4 + 3 = 7$.

Les deux variables aléatoires $T_1$ et $T_2$ sont indépendantes, donc également $V(T) = V(T_1 + T_2) = V(T_1) + V(T_2) = 2 + 1$.

Donc $E(T) = 7$ et $V(T) = 3$.

b) On cherche la probabilité que $5 < T < 9$, ou encore $4 < T - E(T) < 10$.

Cela donne $5 - 7 < T - E(T) < 9 - 7$, c'est-à-dire $-2 < T - E(T) < 2$ ou encore $-3 < T - E(T) < 3$.

Et d'après la question précédente, $-3 < T - E(T) < 3$ et finalement $|T - E(T)| < 3$.

Or $p(5 < T < 9) = 1 - p(|T - E(T)| \geqslant 3)$ car $T - E(T)$ ne prend que des valeurs entières.

En appliquant l'inégalité de Bienaymé-Tchebichev, on a : $p(|T - E(T)| \geqslant 3) \leqslant \frac{V(T)}{3^2} = \frac{3}{9} = \frac{1}{3}$.

D'où : $P(|T - E(T)| < 3) \geqslant 1 - \frac{1}{3}$. Ainsi, on a bien $P(5 \leqslant T \leqslant 9) \geqslant \frac{2}{3}$.

Et donc $p(5 \leqslant T \leqslant 9) \geqslant \frac{2}{3}$.

Exercice 3

Question 1 : Vecteur normal au plan

a) Calculons les coordonnées de $\vec{CA}$ et $\vec{CB}$ :

$$\vec{CA}(x_A - x_C, y_A - y_C, z_A - z_C) = (5; 5; -10)$$

et de même :

$$\vec{CB}(x_B - x_C, y_B - y_C, z_B - z_C) = (0; 0; -\frac{25}{2})$$

Ces deux vecteurs ne sont pas colinéaires (leurs coordonnées ne sont pas proportionnelles).

D'une part : $\vec{n_1} \cdot \vec{CA} = 1 \times 5 - 1 \times 5 + 0 \times (-10) = 0$, donc ces deux vecteurs sont orthogonaux.

D'autre part : $\vec{n_1} \cdot \vec{CB} = 1 \times 0 - 1 \times 0 + 0 \times (-\frac{25}{2}) = 0$, donc ces deux vecteurs sont orthogonaux.

Ainsi, $\vec{n_1}$ est orthogonal à deux vecteurs non colinéaires du plan $(CAD)$.

Donc $\vec{n_1}$ est un vecteur normal au plan $(CAD)$.

b) Comme $\vec{n_1}$ est normal au plan $(CAD)$, ce plan a pour équation cartésienne $x - y + 0z + d = 0$ avec $d \in \mathbb{R}$.

On sait que le point $C$ appartient au plan $(CAD)$ donc $x_C - y_C + d = 0$.

Ainsi, le plan $(CAD)$ a pour équation cartésienne $x - y = 0$.

Question 2 : Intersection d'une droite et d'un plan

a) On sait que ce point $H$ appartient à $\mathcal{D}$ et à $(CAD)$ donc ses coordonnées vérifient les 2 équations.

D'après la représentation paramétrique de $\mathcal{D}$, on a :
$$\begin{cases} x_H = \frac{5}{2}t \\ y_H = 5 - \frac{5}{2}t \\ x_H - y_H = 0 \end{cases}$$

En substituant dans l'équation du plan :
$$\frac{5}{2}t - (5 - \frac{5}{2}t) = 0$$
$$\frac{5}{2}t - 5 + \frac{5}{2}t = 0$$
$$5t = 5$$
$$t = 1$$

Et donc on obtient les coordonnées $H(\frac{5}{2}; \frac{5}{2}; 0)$.

b) Nous devons vérifier que $\vec{BH}$ est orthogonal à $(CAD)$, ou autrement dit qu'il est colinéaire à $\vec{n_1}$.

Calculons :
$$\vec{BH} = \begin{pmatrix} \frac{5}{2} \\ -\frac{5}{2} \\ 0 \end{pmatrix} = \frac{5}{2}\vec{n_1}$$

Cela nous indique bien que $H$ est le projeté orthogonal de $B$ sur $(CAD)$.

Question 3 : Triangle rectangle

a) $A$ et $H$ sont dans le plan $(CAD)$. De plus, $\vec{BH} \perp \vec{AH}$ d'après la question précédente.

Rappel : comme $\vec{BH}$ est orthogonal à $(CAD)$, il est orthogonal à tous les vecteurs de ce plan.

Ainsi $\triangle ABH$ est rectangle en $H$.

b) Notons $\mathcal{A}_{ABH}$ l'aire de $ABH$ (j'utilise cette lettre car on va l'utiliser dans la question suivante !).

On sait que $\triangle ABH$ est rectangle en $H$. Calculons $AH$ et $BH$ :
$$AH^2 = (5 - \frac{5}{2})^2 + (5 - \frac{5}{2})^2 + 0^2 = 2 \times (\frac{5}{2})^2 = \frac{25}{2}$$

Et :
$$BH^2 = (\frac{5}{2})^2 + (\frac{5}{2})^2 + 0^2 = \frac{25}{2}$$

Donc $BH = AH = \frac{5}{\sqrt{2}}$.

L'aire du triangle rectangle $ABH$ est :
$$\mathcal{A}_{ABH} = \frac{AH \times BH}{2} = \frac{1}{2} \times \frac{5}{\sqrt{2}} \times \frac{5}{\sqrt{2}} = \frac{25}{4}$$

L'aire du triangle $ABH$ est bien égale à $\frac{25}{4}$.

Question 4 : Volume d'un tétraèdre

a) On a :

$$\vec{CO} = \begin{pmatrix} 0 \\ 0 \\ 10 \end{pmatrix} \text{ et } \vec{HA} = \begin{pmatrix} \frac{5}{2} \\ \frac{5}{2} \\ 0 \end{pmatrix}$$

Vérifions que $\vec{OC} \cdot \vec{HA} = 0$ et $\vec{OC} \cdot \vec{BH} = 0$ :

$$\vec{OC} \cdot \vec{HA} = 0 \times \frac{5}{2} + 0 \times \frac{5}{2} + 10 \times 0 = 0$$
$$\vec{OC} \cdot \vec{BH} = 0 \times \frac{5}{2} + 0 \times (-\frac{5}{2}) + 10 \times 0 = 0$$

Donc $OC$ est bien orthogonal au plan $(ABH)$, $O \in (ABH)$ et $C \notin (ABH)$.

Donc $(CO)$ est bien la hauteur du tétraèdre $ABCH$ issue de $C$.

b) Compte-tenu des remarques précédentes, le volume du tétraèdre est $\mathcal{V}_{ABCH} = \frac{1}{3} \times$ base $\times$ hauteur.

Notons $h = OC$.

$$\mathcal{V}_{ABCH} = \frac{1}{3} \times \mathcal{A}_{ABH} \times h = \frac{1}{3} \times \frac{25}{4} \times 10 = \frac{125}{6}$$

Et donc l'aire de $ABCH$ est $\mathcal{V}_{ABCH} = \frac{125}{6}$.

Question 5 : Distance d'un point à un plan

Notons $d$ la distance recherchée.

On a $AB = 5$ et $BC = \sqrt{5^2 + 10^2} = \sqrt{125} = 5\sqrt{5}$.

Donc :
$$\frac{1}{3} \times S_{ABC} \times d = \mathcal{V}_{ABCH}$$

où $S_{ABC} = \frac{AB \times BC}{2} = \frac{5 \times 5\sqrt{5}}{2} = \frac{25\sqrt{5}}{2}$.

D'où :
$$d = \frac{3\mathcal{V}_{ABCH}}{S_{ABC}} = \frac{3 \times \frac{125}{6}}{\frac{25\sqrt{5}}{2}} = \frac{\frac{125}{2}}{\frac{25\sqrt{5}}{2}} = \frac{125}{25\sqrt{5}} = \frac{5}{\sqrt{5}} = \sqrt{5}$$

Et finalement la distance de $H$ au plan $(ABC)$ est $d = \sqrt{5}$ (soit environ 2,24).

Exercice 4

Partie A : Étude de la fonction f

Question 1

a) Il n'y a pas de formes indéterminées.

En $x \to 0^+$ :
$$\lim_{x \to 0^+} (x - 2) = -2 \text{ et } \lim_{x \to 0^+} \frac{1}{2}\ln(x) = -\infty$$

Donc, par somme, $\lim_{x \to 0^+} f(x) = -\infty$.

En $x \to +\infty$ :
$$\lim_{x \to +\infty} (x - 2) = +\infty \text{ par somme et } \lim_{x \to +\infty} \frac{1}{2}\ln(x) = +\infty$$

D'où, par somme, $\lim_{x \to +\infty} f(x) = +\infty$.

Et donc $\lim_{x \to 0^+} f(x) = -\infty$ et $\lim_{x \to +\infty} f(x) = +\infty$.

b) $f$ est bien dérivable sur $]0; +\infty[$ comme somme de fonctions qui le sont.

Pour tout $x \in ]0; +\infty[$ :
$$f'(x) = 1 + \frac{1}{2} \times \frac{1}{x} = 1 + \frac{1}{2x} = \frac{2x + 1}{2x}$$

Donc $\forall x \in ]0; +\infty[$, $f'(x) = \frac{2x + 1}{2x}$.

c) Pour tout $x \in ]0; +\infty[$, on a $2x + 1 > 0$ donc $f'(x) > 0$.

Donc $f$ est strictement croissante sur $]0; +\infty[$.

d) On a admis que $f$ est deux fois dérivable sur $]0; +\infty[$.

Pour tout $x \in ]0; +\infty[$ :
$$f''(x) = \frac{2 \times 2x - (2x + 1) \times 2}{4x^2} = \frac{-2}{4x^2} < 0$$

Ainsi $f$ est concave sur $]0; +\infty[$.

Question 2

a) On a le tableau de variations suivant :

Sur $]0; +\infty[$, $f$ est continue (car dérivable) et strictement croissante.

D'autre part : $\lim_{x \to 0^+} f(x) = -\infty$ et $\lim_{x \to +\infty} f(x) = +\infty$.

Donc, d'après le corollaire du théorème des valeurs intermédiaires, l'équation $f(x) = 0$ admet une unique solution sur $]0; +\infty[$.

De plus, $f(1) = 1 - 2 + \frac{1}{2}\ln(1) = -1 < 0$ et $f(2) = 2 - 2 + \frac{1}{2}\ln(2) = \frac{1}{2}\ln(2) > 0$.

On peut donc affirmer que $\alpha \in [1; 2]$.

b) En regroupant les éléments déjà étudiés :

$$\text{Pour tout } x \in ]0; \alpha[, \quad f(x) < 0, \quad f(\alpha) = 0, \quad f(x) > 0$$

On a $\forall x \in ]0; \alpha[$, $f(x) < 0$ et $f(\alpha) = 0$ et $\forall x \in ]\alpha; +\infty[$, $f(x) > 0$.

c) $f(\alpha) = 0$ nous permet d'écrire :

$$\alpha - 2 + \frac{1}{2}\ln(\alpha) = 0$$

ou encore :
$$\frac{1}{2}\ln(\alpha) = 2 - \alpha$$

Et finalement $\ln(\alpha) = 2(2 - \alpha)$.

Partie B : Étude de la fonction g

Question 1

$g$ est bien dérivable sur $]0; 1]$ comme somme et produit de fonctions qui le sont.

Pour tout $x \in ]0; 1]$ :
$$g'(x) = -2 \times \frac{7}{8}x + 1 - \frac{1}{4} \times 2x\ln(x) - \frac{1}{4}x^2 \times \frac{1}{x}$$
$$= -\frac{7}{4}x + 1 - \frac{1}{2}x\ln(x) - \frac{1}{4}x$$
$$g'(x) = -\frac{7}{4}x - \frac{1}{4}x + 1 - \frac{1}{2}x\ln(x) = x\left(\frac{1}{x} - 2 + \frac{1}{2}x\ln\left(\frac{1}{x}\right)\right)$$

Pour tout $x \in ]0; 1]$, $g'(x) = xf\left(\frac{1}{x}\right)$.

Question 2

a) On a $\forall x \in \left]0; \frac{1}{\alpha}\right[$, $\frac{1}{x} \in ]\alpha; +\infty[$.

D'après la question 2.b de la partie A, $\forall x \in ]\alpha; +\infty[$, $f(x) > 0$.

Comme $x > 0$, on a : $xf\left(\frac{1}{x}\right) > 0$.

Et donc $\forall x \in \left]0; \frac{1}{\alpha}\right]$, $xf\left(\frac{1}{x}\right) > 0$.

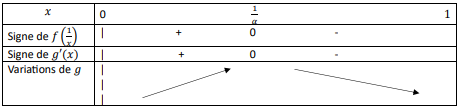
b) D'après la question 1, comme $x \in ]0; 1]$, $g'(x)$ est du signe de $f\left(\frac{1}{x}\right)$.

Tableau de signes :

D'où le tableau de variations :

Valeurs de $x$ : $0 \quad \frac{1}{\alpha} \quad 1$

Signe de $g'(x)$ : $+ \quad 0 \quad -$

Variations de $g$ : croissante puis décroissante

Partie C : Un calcul d'aire

Question 1

a) Soit $h$ la fonction définie sur $]0; 1]$ par $h(x) = g(x) - \left(-\frac{7}{8}x^2 + x\right)$.

Il suffit d'étudier le signe de $h(x)$.

En simplifiant, pour tout $x \in ]0; 1]$ :
$$g(x) + \frac{7}{8}x^2 - x = \frac{1}{4}x^2\ln(x)$$

Or $\forall x \in ]0; 1]$, $\ln(x) \leqslant 0$ donc $g(x) + \frac{7}{8}x^2 - x \leqslant 0$, c'est-à-dire $g(x) \leqslant -\frac{7}{8}x^2 + x$.

Et ainsi, sur $]0; 1]$, $\mathscr{C}_g$ est au-dessous de $\mathscr{P}$.

b) Calculons, en intégrant par parties : $\int_{\frac{1}{a}}^1 x^2\ln(x) dx$

Première méthode :

On pose : $u'(x) = x^2$ et $v(x) = \ln(x)$. On a donc $u(x) = \frac{x^3}{3}$ et $v'(x) = \frac{1}{x}$.

Ainsi :
$$\int_{\frac{1}{a}}^1 x^2\ln(x) dx = \left[\frac{x^3}{3}\ln(x)\right]_{\frac{1}{a}}^1 - \int_{\frac{1}{a}}^1 \frac{x^3}{3} \times \frac{1}{x} dx = -\frac{1}{3a^3}\ln(a) - \int_{\frac{1}{a}}^1 \frac{x^2}{3} dx$$

$$\int_{\frac{1}{a}}^1 x^2\ln(x) dx = \frac{1}{3a^3}2(2-a) - \left[\frac{x^3}{9}\right]_{\frac{1}{a}}^1 = \frac{12-6a}{9a^3} - \frac{1}{9} + \frac{1}{9a^3}$$

Donc : $\int_{\frac{1}{a}}^1 x^2\ln(x) dx = \frac{-a^3-6a+13}{9a^3}$

Question 2

L'aire $\mathcal{A}$ est comprise entre $C_g$ et $\mathscr{P}$ et est donc égale à l'intégrale de la différence des fonctions qu'elles représentent.

Ainsi, cela revient à calculer l'intégrale de $h$ entre $\frac{1}{\alpha}$ et 1.

D'après la question 1.a, on sait que :
$$g(x) - \left(-\frac{7}{8}x^2 + x\right) = \frac{1}{4}x^2\ln(x)$$

Donc :
$$\mathcal{A} = \int_{\frac{1}{\alpha}}^1 \frac{1}{4}x^2\ln(x) dx$$

D'après la question précédente :
$$\mathcal{A} = \frac{1}{4} \times \frac{-\alpha^3 - 6\alpha + 13}{9\alpha^3} = \frac{-\alpha^3 - 6\alpha + 13}{36\alpha^3}$$

Ainsi, d'après la question précédente, $\mathcal{A} = \frac{-\alpha^3 - 6\alpha + 13}{36\alpha^3}$.