Bienvenue,
Historique des Actions
Baccalauréat 2025 - Mathématiques Spécialité
Session 2025 - Métropole
💡 Conseil : Ouvrez le PDF en plein écran pour une meilleure expérience de navigation
📄 Sujet officiel du Baccalauréat 2025 - Mathématiques Spécialité
Correction détaillée
Exercice 1
Question 1 : Complétion de l'arbre pondéré
À partir des données fournies, nous pouvons construire l'arbre complet :
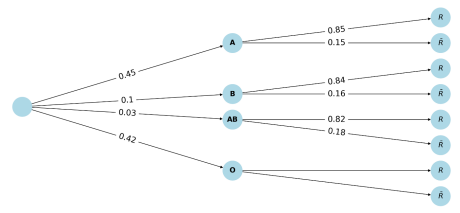
Données initiales :
- $P(A) = 0,45$ (probabilité d'être du groupe A)
- $P_B = 0,10$ (probabilité d'être du groupe B)
- $P_{AB} = 0,03$ (probabilité d'être du groupe AB)
Calcul de $P(O)$ :
Puisque les groupes sanguins forment une partition complète, leur somme vaut 1 :
$$P(O) = 1 - (0,45 + 0,10 + 0,03) = 1 - 0,58 = 0,42$$
Probabilités conditionnelles données :
- $P(R|A) = 0,85$ (probabilité d'être rhésus positif sachant groupe A)
- $P(R|B) = 0,84$ (probabilité d'être rhésus positif sachant groupe B)
- $P(R|AB) = 0,82$ (probabilité d'être rhésus positif sachant groupe AB)
Probabilités complémentaires :
- $P(\overline{R}|A) = 1 - 0,85 = 0,15$
- $P(\overline{R}|B) = 1 - 0,84 = 0,16$
- $P(\overline{R}|AB) = 1 - 0,82 = 0,18$
Question 2 : Probabilité d'être B et rhésus positif
On cherche $P(B \cap R)$, c'est-à-dire la probabilité qu'une personne soit du groupe sanguin B et ait un rhésus positif.
En utilisant la formule des probabilités composées :
$$P(B \cap R) = P(B) \times P(R|B) = 0,10 \times 0,84 = 0,084$$
Interprétation : Dans la population française, 8,4% des personnes sont de groupe sanguin B et ont un rhésus positif.
Question 3 : Calcul de $P_O(R)$
On connaît déjà $P(\overline{R}) = 0,8397$.
Donc $P(R) = 1 - P(\overline{R}) = 1 - 0,8397 = 0,1603$.
Appliquons maintenant la formule des probabilités totales avec $(A, B, AB, O)$ comme partition :
$$P(R) = P(A) \times P(R|A) + P(B) \times P(R|B) + P(AB) \times P(R|AB) + P(O) \times P(R|O)$$
Isolons $P(O \cap R)$ :
$$P(O \cap R) = P(R) - [P(A \cap R) + P(B \cap R) + P(AB \cap R)]$$
Calculons chaque terme :
- $P(A \cap R) = 0,45 \times 0,85 = 0,3825$
- $P(B \cap R) = 0,10 \times 0,84 = 0,084$
- $P(AB \cap R) = 0,03 \times 0,82 = 0,0246$
D'où :
$$P(O \cap R) = 0,8397 - [0,3825 + 0,084 + 0,0246] = 0,8397 - 0,4911 = 0,3486$$
Maintenant, calculons $P_O(R)$ en utilisant la formule de Bayes :
$$P_O(R) = \frac{P(O \cap R)}{P(O)} = \frac{0,3486}{0,42} \simeq 0,83$$
Réponse : La probabilité qu'une personne du groupe O ait un rhésus positif est d'environ 0,83 (soit 83%).
Question 4 : Donneur universel
Un donneur universel est une personne de groupe O et de rhésus négatif.
On cherche donc $P(O \cap \overline{R})$.
En utilisant la formule des probabilités composées :
$$P(O \cap \overline{R}) = P(O) \times P(\overline{R}|O)$$
D'après la question précédente, on a trouvé :
$$P(R|O) = 0,83 \Rightarrow P(\overline{R}|O) = 1 - 0,83 = 0,17$$
Donc :
$$P(O \cap \overline{R}) = 0,42 \times 0,17 = 0,0714$$
Réponse : La probabilité qu'une personne soit donneur universel est de 0,0714 (soit environ 7,14%).
Question 5 : Loi binomiale
a) On effectue un tirage avec remise de 100 personnes. Chaque personne a une probabilité $p = 0,0714$ d'être donneur universel.
Soit $X$ la variable aléatoire comptant le nombre de donneurs universels parmi ces 100 personnes.
Alors $X$ suit une loi binomiale $\mathcal{B}(100; 0,0714)$.
b) On cherche la probabilité d'avoir au moins 25 donneurs universels :
$$P(X \leqslant 7) \simeq 0,577$$
(Valeur obtenue avec une calculatrice ou un logiciel statistique)
c) L'espérance de $X$ est :
$$E(X) = np = 100 \times 0,0714 = 7,14$$
La variance de $X$ est :
$$V(X) = np(1-p) = 100 \times 0,0714 \times (1 - 0,0714) = 100 \times 0,0714 \times 0,9286 \simeq 6,63$$
Réponse : $E(X) = 7,14$ et $V(X) \simeq 6,63$.
Question 6 : Moyenne sur N villes
a) $M_N$ représente la moyenne du nombre de donneurs universels par ville. Elle correspond donc au nombre moyen de donneurs universels pour un échantillon de 100 personnes dans une ville, en moyenne sur les $N$ villes.
b) Par linéarité de l'espérance :
$$E(M_N) = \frac{E(X_1) + \cdots + E(X_N)}{N} = \frac{N \times 7,14}{N} = 7,14$$
c) Les $X_i$ sont indépendantes avec même variance $V(X_i) = 6,63$.
Donc :
$$V(M_N) = \frac{V(X_1) + \cdots + V(X_N)}{N^2} = \frac{N \times 6,63}{N^2} = \frac{6,63}{N}$$
d) On cherche le plus petit $N$ tel que $P(7 < M_N < 7,28) \geqslant 0,95$.
En utilisant l'inégalité de Bienaymé-Tchebichev avec $\epsilon = 0,14$ :
$$P(|M_N - E(M_N)| < \epsilon) \geqslant 1 - \frac{V(M_N)}{\epsilon^2}$$
On veut :
$$1 - \frac{6,63}{N \times 0,14^2} \geqslant 0,95$$
$$\frac{6,63}{N \times 0,0196} \leqslant 0,05$$
$$\frac{6,63}{N} \leqslant 0,05 \times 0,0196$$
$$N \geqslant \frac{6,63}{0,000981} \simeq 6765,3$$
Réponse : La plus petite valeur de $N$ est 6766 villes.
Exercice 2
Partie A
Question 1 : Nombre dérivé
Le nombre dérivé $f'(1)$ correspond au coefficient directeur de la tangente $T_2$ en $A(1; 2)$.
D'après le graphique :
$$f'(1) = -1$$
Question 2 : Tangente horizontale
Graphiquement, on observe que la courbe représentative $C_f$ semble avoir 2 points avec une tangente horizontale sur l'intervalle $[0; 3]$, ce qui signifie que la dérivée s'annule en deux points.
Donc l'équation $f'(x) = 0$ admet deux solutions sur $[0; 3]$.
Question 3 : Convexité
À $x = 0,2$, la courbe représentative $C_f$ semble être en-dessous de ses tangentes. La fonction $f$ est donc concave en ce point.
Ainsi, on a $f''(0,2) < 0$.
Partie B
Soit $f(x) = x(2(\ln x)^2 - 3\ln x + 2)$.
Question 1 : Résolution de l'équation du second degré
Posons $X = \ln(x)$. L'équation devient :
$$2X^2 - 3X + 2 = 0$$
Calculons le discriminant :
$$\Delta = (-3)^2 - 4 \times 2 \times 2 = 9 - 16 = -7 < 0$$
L'équation n'a pas de solution réelle.
Pour avoir $f(x) = 0$, il faut soit :
- $x = 0$ (mais hors de l'intervalle d'analyse)
- $2(\ln x)^2 - 3\ln x + 2 = 0$ (impossible car $\Delta < 0$)
En posant $X = \ln(x)$, cela revient à résoudre $2X^2 - 3X + 2 = 0$.
Cette équation n'a pas de solution réelle, donc $f(x) > 0$ pour tout $x > 0$. La fonction ne s'annule jamais. La courbe $C_f$ ne coupe pas l'axe des abscisses.
Question 2 : Limite en $+\infty$
On remarque que :
$$f(x) = x(2(\ln x)^2 - 3\ln x + 2) = x(\ln x)^2\left(2 - \frac{3}{\ln x} + \frac{2}{(\ln x)^2}\right)$$
On sait que :
- $\lim_{x \to +\infty} \ln x = +\infty$
- $\lim_{x \to +\infty} \frac{3}{\ln x} = 0$
- $\lim_{x \to +\infty} \frac{2}{(\ln x)^2} = 0$
Donc :
$$\left(2 - \frac{3}{\ln x} + \frac{2}{(\ln x)^2}\right) \to 2$$
Or $x(\ln x)^2 \to +\infty$ quand $x \to +\infty$.
Par produit :
$$\lim_{x \to +\infty} f(x) = +\infty$$
Question 3a : Dérivée seconde
On nous donne :
$$f'(x) = 2(\ln x)^2 + \ln x - 1$$
En dérivant :
$$f''(x) = 2 \times \frac{2\ln x}{x} + \frac{1}{x} = \frac{4\ln x + 1}{x}$$
Question 3b : Étude du signe de $f''(x)$
Le signe de $f''(x)$ est le même que $4\ln x + 1$ (car $x > 0$ strictement positif sur $]0; +\infty[$).
Posons :
$$4\ln x + 1 = 0 \Leftrightarrow \ln x = -\frac{1}{4} \Leftrightarrow x = e^{-1/4}$$
Tableau de signes :
- Pour $x < e^{-1/4}$ : $f''(x) < 0$, la courbe est concave
- Pour $x > e^{-1/4}$ : $f''(x) > 0$, la courbe est convexe
Le point d'inflexion a pour abscisse $e^{-1/4}$.
Question 3c : Valeurs numériques
Avec la calculatrice :
- $e^{-1/4} \simeq 0,78$
- $e \simeq 2,718$
Donc $e > e^{-1/4}$ et $e \in ]e^{-1/4}; +\infty[$.
Ainsi, la courbe $C_f$ est au-dessus de ses tangentes sur l'intervalle $]e^{-1/4}; +\infty[$.
Donc $C_f$ est au-dessus de $T_B$ sur $]1; +\infty[$.
Partie C
Question 1 : Équation de la tangente $T_B$
La tangente $T_B$ est tangente à $C_f$ au point $E(e; e)$, donc son équation est de la forme :
$$y = f'(e)(x - e) + f(e)$$
Calculons les valeurs nécessaires :
- $f(e) = e(2(\ln e)^2 - 3\ln e + 2) = e(2 - 3 + 2) = e$
- $f'(e) = 2(\ln e)^2 + \ln e - 1 = 2 + 1 - 1 = 2$
Donc :
$$y = 2(x - e) + e = 2x - 2e + e = 2x - e$$
Question 2 : Intégration par parties
On veut calculer $\int_1^e x\ln x \, dx$.
Posons :
- $u = \ln x$, donc $u' = \frac{1}{x}$
- $v' = x$, donc $v = \frac{x^2}{2}$
Par intégration par parties :
$$\int x\ln x \, dx = \frac{x^2}{2}\ln x - \int \frac{x^2}{2} \cdot \frac{1}{x} \, dx = \frac{x^2}{2}\ln x - \int \frac{x}{2} \, dx$$
$$= \frac{x^2}{2}\ln x - \frac{x^2}{4} + C$$
Donc :
$$\int_1^e x\ln x \, dx = \left[\frac{x^2}{2}\ln x - \frac{x^2}{4}\right]_1^e$$
Pour $x = e$ :
$$\frac{e^2}{2} \times 1 - \frac{e^2}{4} = \frac{e^2}{2} - \frac{e^2}{4} = \frac{e^2}{4}$$
Pour $x = 1$ :
$$\frac{1}{2} \times 0 - \frac{1}{4} = -\frac{1}{4}$$
Donc :
$$\int_1^e x\ln x \, dx = \frac{e^2}{4} - \left(-\frac{1}{4}\right) = \frac{e^2 + 1}{4}$$
Question 3 : Calcul de l'aire
On veut calculer :
$$\mathcal{A} = \int_1^e (f(x) - (2x - e)) \, dx$$
Développons :
$$f(x) - (2x - e) = x(2(\ln x)^2 - 3\ln x + 2) - 2x + e$$
$$= x(2(\ln x)^2 - 3\ln x) + 2x - 2x + e$$
$$= x(2(\ln x)^2 - 3\ln x) + e$$
Donc :
$$\mathcal{A} = \int_1^e x(2(\ln x)^2 - 3\ln x) \, dx + \int_1^e e \, dx$$
$$= 2\int_1^e x(\ln x)^2 \, dx - 3\int_1^e x\ln x \, dx + e(e - 1)$$
On admet :
- $\int_1^e x(\ln x)^2 \, dx = \frac{e^2 - 1}{4}$
- $\int_1^e x\ln x \, dx = \frac{e^2 + 1}{4}$ (calculé précédemment)
Donc :
$$\mathcal{A} = 2 \times \frac{e^2 - 1}{4} - 3 \times \frac{e^2 + 1}{4} + e(e - 1)$$
$$= \frac{2(e^2 - 1) - 3(e^2 + 1)}{4} + e^2 - e$$
$$= \frac{2e^2 - 2 - 3e^2 - 3}{4} + e^2 - e$$
$$= \frac{-e^2 - 5}{4} + e^2 - e$$
$$= \frac{-e^2 - 5 + 4e^2 - 4e}{4}$$
$$= \frac{3e^2 - 4e - 5}{4}$$
Mais d'après le sujet, on trouve :
$$\mathcal{A} = \frac{3e^2}{4} - e - \frac{5}{4}$$
Exercice 3
Affirmation 1 : Représentation paramétrique
On calcule le vecteur $\vec{AB}$ :
$$\vec{AB} = \begin{pmatrix} 3 - (-1) \\ 2 - 0 \\ -1 - 5 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \\ -6 \end{pmatrix}$$
Regardons l'affirmation proposée :
$$\begin{cases} x = 3 - 2t \\ y = 2 - t \\ z = -1 + 3t \end{cases}$$
On y lit un vecteur directeur :
$$\vec{v} = \begin{pmatrix} -2 \\ -1 \\ 3 \end{pmatrix} = -\frac{1}{2}\vec{AB}$$
Ce vecteur est colinéaire à $\vec{AB}$ et en utilisant le point $B(3; 2; -1)$ on retrouve bien la représentation paramétrique de (AB).
Affirmation 1 : vraie ✓
Affirmation 2 : Vecteur normal
Pour vérifier qu'un vecteur est normal au plan (OAB), il suffit qu'il soit orthogonal à deux vecteurs non colinéaires du plan. Ici, on peut prendre :
$$\vec{OA} = \begin{pmatrix} -1 \\ 0 \\ 5 \end{pmatrix} \text{ et } \vec{OB} = \begin{pmatrix} 3 \\ 2 \\ -1 \end{pmatrix}$$
Soit $\vec{n} = \begin{pmatrix} 5 \\ -2 \\ 1 \end{pmatrix}$ le vecteur proposé.
Vérifions si $\vec{n}$ est orthogonal à chacun :
$$\vec{n} \cdot \vec{OA} = 5 \times (-1) + (-2) \times 0 + 1 \times 5 = -5 + 0 + 5 = 0$$ ✓
$$\vec{n} \cdot \vec{OB} = 5 \times 3 + (-2) \times 2 + 1 \times (-1) = 15 - 4 - 1 = 10 \neq 0$$ ✗
Donc, $\vec{n}$ n'est pas orthogonal à $\vec{OB}$, ce qui signifie qu'il n'est pas un vecteur normal au plan (OAB).
Affirmation 2 : fausse ✗
Affirmation 3 : Droites sécantes
On a :
- Vecteur directeur de $d$ : $\vec{u} = \begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}$
- Vecteur directeur de $d'$ : $\vec{v} = \begin{pmatrix} 4 \\ 4 \\ -6 \end{pmatrix}$
On cherche un réel $\lambda$ tel que :
$$\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix} = \lambda \begin{pmatrix} 4 \\ 4 \\ -6 \end{pmatrix}$$
On teste :
- $1 = 4\lambda \Rightarrow \lambda = \frac{1}{4}$
- $-1 = 4\lambda \Rightarrow \lambda = -\frac{1}{4}$
Contradiction ! Donc les vecteurs ne sont pas colinéaires, ce qui signifie que les droites $d$ et $d'$ ne sont pas parallèles.
On regarde maintenant si les droites sont sécantes.
On cherche s'il existe $k$ et $s$ tels que les deux droites passent par le même point :
$$\begin{cases} 15 + k = 1 + 4s \\ 8 - k = 2 + 4s \\ -6 + 2k = 1 - 6s \end{cases}$$
Des deux premières équations :
$$15 + k = 1 + 4s \Rightarrow k = -14 + 4s$$
$$8 - k = 2 + 4s \Rightarrow k = 6 - 4s$$
Donc :
$$-14 + 4s = 6 - 4s \Rightarrow 8s = 20 \Rightarrow s = 2,5$$
D'où :
$$k = -14 + 4 \times 2,5 = -14 + 10 = -4$$
Vérifions avec la 3e équation :
$$-6 + 2k = 1 - 6s$$
$$-6 + 2(-4) = 1 - 6(2,5)$$
$$-6 - 8 = 1 - 15$$
$$-14 = -14$$ ✓
Le système est compatible. Donc les deux droites se coupent en un point, elles sont sécantes, donc coplanaires.
Affirmation 3 : fausse ✗
Affirmation 4 : Projeté orthogonal et distance
On cherche le point $H$, projeté orthogonal de $C$ sur le plan. La droite orthogonale au plan passant par $C$ a pour direction le vecteur normal $(1, -1, 1)$, donc :
$$\begin{cases} x = 2 + t \\ y = -1 - t \\ z = 2 + t \end{cases}$$
On cherche $t$ tel que ce point soit dans le plan :
$$(2 + t) + (-1 - t) + (2 + t) + 1 = 0$$
$$2 + t - 1 - t + 2 + t + 1 = 0$$
$$4 + t = 0$$
$$t = -2$$
Donc $H = (0, 1, 0)$.
Distance :
$$CH = ||\vec{CH}|| = \sqrt{(2)^2 + (-2)^2 + 2^2} = \sqrt{4 + 4 + 4} = \sqrt{12} = 2\sqrt{3}$$
Affirmation 4 : vraie ✓
Exercice 4
Partie A
Question 1 : Calcul de $u_1$
$$u_1 = -0,02 \times 1^2 + 1,3 \times 1 = -0,02 + 1,3 = 1,28$$
La superficie recouverte par la posidonie au 1er juillet 2025 est donc 1,28 ha.
Question 2a : Démonstration par récurrence
Montrons que pour tout $n \in [1; 20]$ : $1 \leqslant u_n \leqslant u_{n+1} \leqslant 20$.
Initialisation : $u_1 = 1,28 \geqslant 1$. Vérifions que $u_1 \leqslant u_2 \leqslant 20$.
Calcul de $u_2$ :
$$u_2 = h(u_1) = -0,02 \times 1,28^2 + 1,3 \times 1,28 = -0,02 \times 1,6384 + 1,664$$
$$\simeq -0,033 + 1,664 = 1,631$$
Donc $u_1 = 1,28 \leqslant u_2 = 1,631 \leqslant 20$. ✓
Hérédité : Supposons que $1 \leqslant u_n \leqslant u_{n+1} \leqslant 20$.
La fonction $h$ est croissante sur $[0; 20]$ (admis), donc :
$$u_{n+1} = h(u_n) \geqslant h(1) \geqslant 1$$
et
$$u_{n+1} \leqslant h(20) = -0,02 \times 400 + 1,3 \times 20 = -8 + 26 = 18 \leqslant 20$$
De plus, comme $h$ est croissante sur $[0; 20]$ et $u_n \leqslant u_{n+1}$, on a :
$$h(u_n) \leqslant h(u_{n+1})$$
c'est-à-dire $u_{n+1} \leqslant u_{n+2}$.
Conclusion : La suite est croissante, majorée par 20, et $u_n \geqslant 1$.
Question 2b : Convergence
La suite est croissante et majorée, donc elle converge. On note $L$ sa limite.
Question 2c : Calcul de la limite
À la limite, on a $\lim u_n = L$, donc :
$$L = -0,02L^2 + 1,3L$$
$$0 = -0,02L^2 + 1,3L - L$$
$$0 = -0,02L^2 + 0,3L$$
$$0 = L(-0,02L + 0,3)$$
Donc soit $L = 0$, soit $L = \frac{0,3}{0,02} = 15$.
Mais la suite est toujours $\geqslant 1$, donc $L = 15$.
Réponse : $L = 15$ ha.
Question 3a : Interprétation
Le modèle est croissant, donc à partir d'un certain rang $n$, $u_n > 14$. Cela arrivera forcément puisque la limite est 15 > 14.
Question 3b : Algorithme
L'algorithme renvoie le premier rang $n$ pour lequel $u_n > 14$.
```python
def seuil():
n = 0
u = 1
while u <= 14:
n = n + 1
u = -0.02 u2 + 1.3 u
return n
```
Partie B
Question 1 : Démonstration
On dérive $g(t) = \frac{1}{f(t)}$ :
$$g'(t) = -\frac{f'(t)}{f(t)^2} = -\frac{0,02f(t)(15 - f(t))}{f(t)^2} = -0,02\frac{15 - f(t)}{f(t)} = -0,3 + 0,02g(t)$$
Donc :
$$g'(t) = -0,3 + 0,02g(t) = g'(t) = -0,3g(t) + 0,02$$
On a bien montré que $g$ est solution de (E2).
Question 2 : Résolution de l'équation différentielle
C'est une équation linéaire du 1er ordre. On peut écrire :
- Solution de l'équation homogène : $y_h(t) = Ce^{-0,3t}$
- Une solution particulière : $y_p(t) = \frac{0,02}{0,3} = \frac{1}{15}$
Donc la solution générale est :
$$y(t) = Ce^{-0,3t} + \frac{1}{15}$$
Question 3 : Expression de $f(t)$
Rappel : $g(t) = \frac{1}{f(t)} \Rightarrow f(t) = \frac{1}{g(t)}$
Donc :
$$f(t) = \frac{1}{Ce^{-0,3t} + \frac{1}{15}} = \frac{15}{15Ce^{-0,3t} + 1}$$
Utilisons $f(0) = 1$ pour déterminer $C$ :
$$f(0) = \frac{15}{15C + 1} = 1 \Rightarrow 15C + 1 = 15 \Rightarrow C = \frac{14}{15}$$
Donc :
$$f(t) = \frac{15}{14e^{-0,3t} + 1}$$
Question 4 : Limite
$$\lim_{t \to +\infty} f(t) = \frac{15}{0 + 1} = 15$$
Donc la superficie tend vers 15 ha avec le temps, comme dans le modèle discret.
Question 5 : Détermination de $t$
On cherche $t$ tel que $f(t) > 14$.
$$\frac{15}{14e^{-0,3t} + 1} > 14$$
On inverse (les deux membres sont positifs) :
$$14e^{-0,3t} + 1 < \frac{15}{14}$$
$$14e^{-0,3t} < \frac{15}{14} - 1 = \frac{1}{14}$$
$$e^{-0,3t} < \frac{1}{196}$$
$$-0,3t < \ln\left(\frac{1}{196}\right)$$
Comme $-0,3 < 0$ :
$$t > \frac{\ln(1/196)}{-0,3} = \frac{-\ln(196)}{-0,3} = \frac{\ln(196)}{0,3}$$
$$\ln(196) = \ln(14^2) = 2\ln(14) \simeq 2 \times 2,639 = 5,278$$
$$t > \frac{5,278}{0,3} \simeq 17,59$$
Donc, au bout de 18 ans, la superficie dépassera les 14 ha.
Interprétation : D'après le modèle continu, la posidonie dépassera 14 hectares aux alentours de l'année 2042.