Angles
Sixieme
Les Angles
Introduction
Un angle est l'ouverture formée par deux demi-droites de même origine. Les angles sont partout autour de nous : dans les coins des pièces, les aiguilles d'une horloge, les branches d'un arbre... Comprendre les angles est essentiel pour la géométrie et de nombreuses applications pratiques.
A) Définitions et notations
Définition fondamentale
Un angle est l'ouverture formée par deux demi-droites de même origine.
Notation et vocabulaire
La demi-droite d'origine A passant par E est notée \([AE)\).
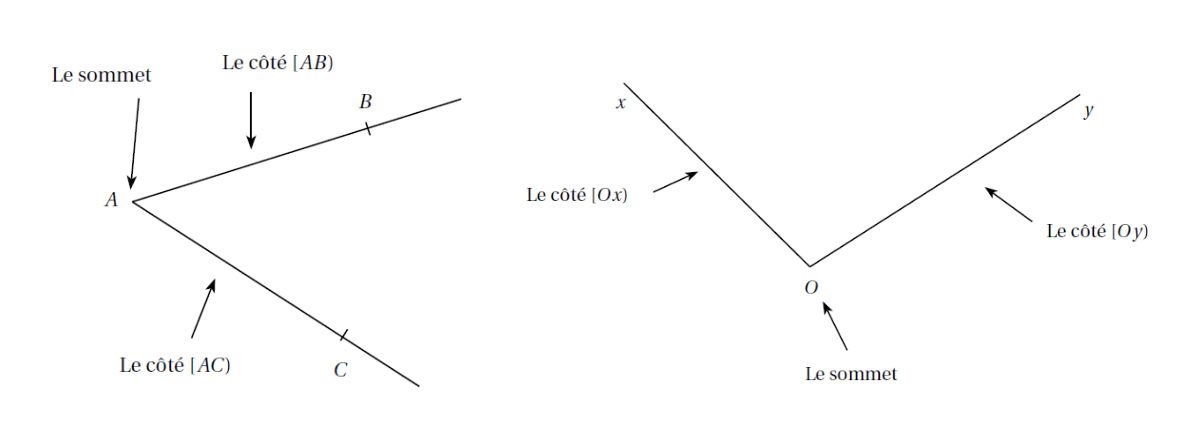
Vocabulaire :• Les demi-droites sont les côtés de l'angle
• Leur origine est le sommet de l'angle
Exemples concrets
Sur la figure ci-dessous, on a tracé l'angle BAC (ou CAB) et l'angle xOy (ou yOx).
B) Mesure d'un angle
Définition de l'unité
Comme pour les longueurs, on choisit une unité d'angle pour pouvoir comparer numériquement les angles.
Le degré (noté \(°\)) est l'unité usuelle des angles depuis plus de 4000 ans. Il correspond à la 360ème partie d'un cercle.
Propriétés fondamentales
• Deux angles sont égaux s'ils ont la même ouverture (même mesure). Ils peuvent alors se superposer.
• Dans un triangle, la somme des trois angles est égale à \(180°\).
On peut utiliser du papier calque pour comparer des angles.
Exemple de calcul
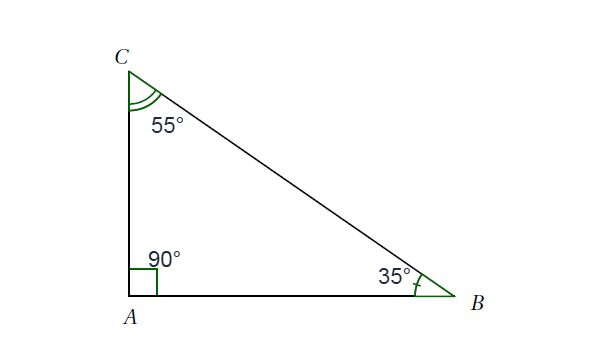
Sur la figure ci-dessous, l'angle BAC est un angle droit (\(90°\)), l'angle ACB mesure \(55°\) et l'angle ABC mesure \(35°\).
Calcul : \(55° + 90° + 35° = 180°\)
Conclusion : Si l'on additionne la mesure de chaque angle, cela donne bien \(180°\).
C) Classification des angles
Vocabulaire et catégories
On classe les angles par catégories selon leur mesure :
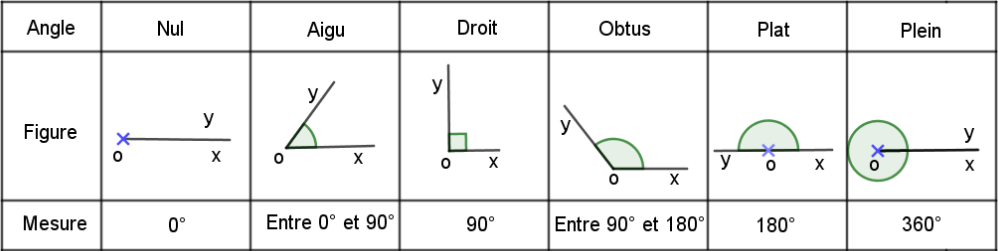
• Angle nul : \(0°\)
• Angle aigu : entre \(0°\) et \(90°\)
• Angle droit : \(90°\)
• Angle obtus : entre \(90°\) et \(180°\)
• Angle plat : \(180°\)
• Angle plein : \(360°\)
D) Angles adjacents
Définition
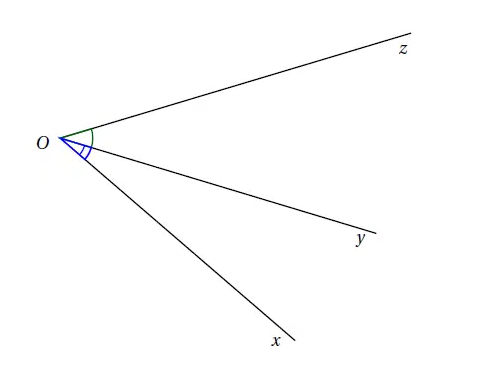
Deux angles adjacents ont le même sommet, un côté en commun et sont situés de part et d'autre de ce côté.
Exemple concret
Sur la figure ci-dessous, les angles xOy et yOz sont adjacents.
E) Bissectrice d'un angle
Définition
La bissectrice d'un angle est la demi-droite qui partage cet angle en deux angles adjacents de même mesure.
Exemple de calcul
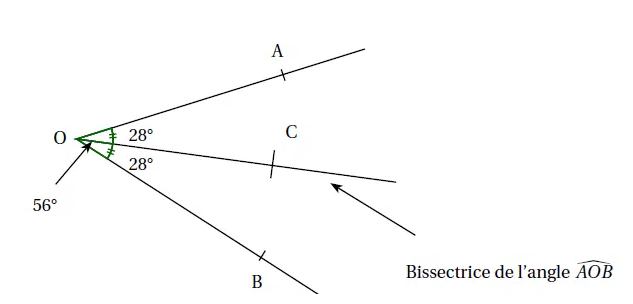
L'angle AOB mesure \(56°\). Sa bissectrice, la demi-droite \([OC)\), le partage en deux angles de \(28°\).
Donnée : \(\angle AOB = 56°\)
Calcul : \(\frac{56°}{2} = 28°\)
Conclusion : La bissectrice partage l'angle en deux angles de \(28°\) chacun.
Applications pratiques
• L'architecture : pour dessiner des plans
• La navigation : pour se diriger
• Le sport : pour calculer des trajectoires
• L'art : pour créer des perspectives
Résumé
• Un angle est formé par deux demi-droites de même origine
• L'unité de mesure est le degré (\(°\))
• Il existe 6 types d'angles : nul, aigu, droit, obtus, plat, plein
• La bissectrice partage un angle en deux parties égales
• Dans un triangle, la somme des angles est \(180°\)