Les Fractions

Introduction

Les fractions permettent de représenter des parties d'un tout. Elles sont partout dans notre vie quotidienne : partager une pizza, mesurer des ingrédients en cuisine, calculer des pourcentages...

A) Quotient et fraction

Définition

Une fraction est l'écriture fractionnaire du quotient de deux nombres.

Si b est un nombre non nul, l'écriture fractionnaire du quotient a ÷ b est a/b.

Si a et b sont des nombres entiers, alors le nombre a/b est appelé une fraction.

Remarque importante

Une fraction EST UN NOMBRE mais pas toujours un nombre décimal.

Exemples

• Le quotient de 14 par 5 est égal à $\frac{14}{5}$. Or 14 ÷ 5 = 2,8. Donc on a : $\frac{14}{5}$ = 14 ÷ 5 = 2,8.
• Le quotient de 2 par 3 est égal à $\frac{2}{3}$. Or 2 ÷ 3 ≈ 0,667... la division ne se termine pas. Donc $\frac{2}{3}$ n'a pas d'écriture décimale.

Représentation sur une demi-droite graduée

On peut utiliser des fractions pour repérer un point sur une demi-droite graduée.

Exemple : L'abscisse de A est $\frac{1}{4}$ et celle de B est $\frac{11}{4}$ ou 2,75.

B) Prendre la fraction d'une quantité

Propriété

Prendre la fraction d'un nombre, c'est multiplier ce nombre par la fraction.

Exemple

Pour prendre les $\frac{3}{5}$ de 85, on effectue le calcul : $\frac{3}{5}$ × 85

Méthode

1. On commence par chercher un cinquième de 85 → 85 ÷ 5 = 17
2. Trois cinquièmes de 85, c'est 3 fois 1 cinquième de 85 → 3 × 17 = 51

Illustration pratique

C) Fractions égales

Définition

Deux fractions sont égales si on peut passer de l'une à l'autre en multipliant (ou en divisant) le numérateur ET le dénominateur par un même nombre non nul.

Remarque

Deux fractions égales ont la même écriture décimale lorsque celle-ci existe.

Exemple

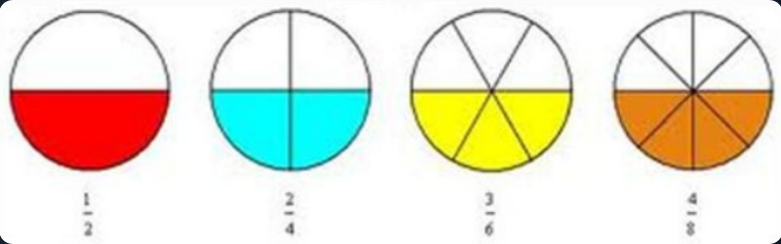
Les fractions $\frac{1}{2}$, $\frac{2}{4}$, $\frac{3}{6}$ et $\frac{4}{8}$ sont égales car :
$\frac{1}{2}$ = $\frac{1 \times 2}{2 \times 2}$ = $\frac{2}{4}$ = $\frac{2 \times 3}{4 \times 3}$ = $\frac{6}{12}$ = $\frac{6 \div 2}{12 \div 2}$ = $\frac{3}{6}$ = $\frac{3 \times 4}{6 \times 4}$ = $\frac{12}{24}$ = $\frac{12 \div 3}{24 \div 3}$ = $\frac{4}{8}$

D) Simplifier une fraction

Définition

Simplifier une fraction c'est trouver la fraction égale dont le numérateur et le dénominateur sont des nombres entiers les plus petits possibles.

Exemple

Simplifier la fraction $\frac{36}{24}$ :
$\frac{36}{24}$ = $\frac{36 \div 4}{24 \div 4}$ = $\frac{9}{6}$ = $\frac{9 \div 3}{6 \div 3}$ = $\frac{3}{2}$

Méthode de simplification

1. Chercher un diviseur commun au numérateur et au dénominateur
2. Diviser le numérateur et le dénominateur par ce diviseur
3. Répéter jusqu'à ce qu'il n'y ait plus de diviseur commun autre que 1

E) Comparaison de fractions

Fractions de même dénominateur

Quand deux fractions ont le même dénominateur, la plus grande est celle qui a le plus grand numérateur.

Exemple : $\frac{3}{7}$ < $\frac{5}{7}$ car 3 < 5

Fractions de même numérateur

Quand deux fractions ont le même numérateur, la plus grande est celle qui a le plus petit dénominateur.

Exemple : $\frac{3}{4}$ > $\frac{3}{5}$ car 4 < 5

Cas général

Pour comparer deux fractions, on peut :

1. Les mettre au même dénominateur
2. Ou les convertir en nombres décimaux

F) Addition et soustraction de fractions

Fractions de même dénominateur

Pour additionner ou soustraire des fractions de même dénominateur, on garde le dénominateur et on additionne ou soustrait les numérateurs.

Exemples :

• $\frac{2}{5}$ + $\frac{1}{5}$ = $\frac{3}{5}$
• $\frac{7}{8}$ - $\frac{3}{8}$ = $\frac{4}{8}$ = $\frac{1}{2}$

Fractions de dénominateurs différents

Il faut d'abord les mettre au même dénominateur (le plus petit commun multiple).

Exemple : $\frac{1}{3}$ + $\frac{1}{4}$

• Le PPCM de 3 et 4 est 12
• $\frac{1}{3}$ = $\frac{4}{12}$ et $\frac{1}{4}$ = $\frac{3}{12}$
• $\frac{1}{3}$ + $\frac{1}{4}$ = $\frac{4}{12}$ + $\frac{3}{12}$ = $\frac{7}{12}$

G) Multiplication de fractions

Règle

Pour multiplier deux fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.

Formule : $\frac{a}{b}$ × $\frac{c}{d}$ = $\frac{a \times c}{b \times d}$

Exemples

• $\frac{2}{3}$ × $\frac{3}{4}$ = $\frac{2 \times 3}{3 \times 4}$ = $\frac{6}{12}$ = $\frac{1}{2}$
• $\frac{1}{2}$ × $\frac{1}{3}$ = $\frac{1 \times 1}{2 \times 3}$ = $\frac{1}{6}$

Interprétation géométrique

Multiplier par une fraction, c'est prendre cette fraction du nombre.

Applications pratiques

Dans la vie quotidienne

• Cuisine : $\frac{3}{4}$ de tasse de farine
• Mesures : $\frac{1}{2}$ mètre de tissu
• Temps : $\frac{1}{4}$ d'heure = 15 minutes
• Argent : $\frac{1}{5}$ de 100€ = 20€

En géométrie

• Aires : $\frac{1}{2}$ × base × hauteur
• Volumes : $\frac{1}{3}$ × aire de base × hauteur
• Angles : $\frac{1}{4}$ de tour = 90°

Résumé

• Une fraction est l'écriture fractionnaire d'un quotient
• Prendre une fraction d'un nombre, c'est le multiplier par cette fraction
• Deux fractions sont égales si on peut passer de l'une à l'autre en multipliant numérateur et dénominateur par le même nombre
• Simplifier une fraction, c'est la réduire à sa forme la plus simple
• Pour additionner/soustraire des fractions, on les met au même dénominateur
• Pour multiplier des fractions, on multiplie les numérateurs et les dénominateurs
• Les fractions sont partout dans notre vie quotidienne !

Exercices d'application

1. Simplifier $\frac{24}{36}$
2. Calculer $\frac{2}{3}$ + $\frac{1}{4}$
3. Calculer $\frac{3}{5}$ × $\frac{2}{7}$
4. Comparer $\frac{4}{7}$ et $\frac{5}{8}$
5. Prendre les $\frac{2}{3}$ de 45
6. Représenter $\frac{3}{4}$ sur une droite graduée