Geometrie Figures Planes
Sixieme
Les Figures Géométriques Planes
Introduction
La géométrie plane explore les formes à deux dimensions qui se dessinent sur une surface plane. Cette discipline nous aide à comprendre les propriétés des formes, leurs relations et leurs applications dans le monde qui nous entoure. Nous allons découvrir les formes de base : le cercle, les triangles et les quadrilatères.
1) Le cercle et ses éléments
Définition fondamentale
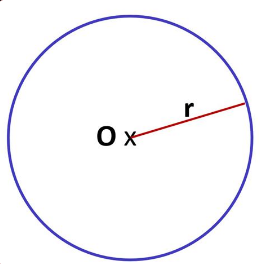
Un cercle est l'ensemble de tous les points situés à une distance fixe (appelée rayon) d'un point central (appelé centre).
Pour dessiner un cercle, on utilise un compas. On règle l'écartement à la longueur du rayon, on place la pointe sur le centre et on trace la courbe.
Les éléments du cercle
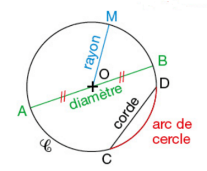
• Rayon : Segment qui relie le centre à n'importe quel point de la courbe (exemple : \([OM]\))
• Diamètre : Segment qui traverse le centre et relie deux points opposés de la courbe (exemple : \([AB]\))
• Corde : Segment qui joint deux points de la courbe sans passer par le centre (exemple : \([CD]\))
• Arc : Portion de la courbe entre deux points, notée \(\widehat{CD}\)
La longueur du diamètre est toujours le double de celle du rayon : \(d = 2r\)
Les propriétés fondamentales
Tous les points d'un cercle sont équidistants du centre.

Si deux points sont à la même distance d'un point central, alors ils appartiennent au même cercle centré sur ce point.

2) Les triangles et leurs variétés
Notion de base
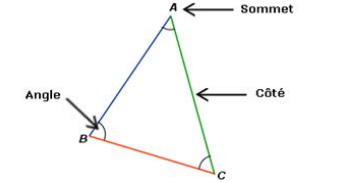
Un triangle est une figure géométrique formée de trois segments de droite qui se rejoignent trois par trois.
Un triangle possède trois angles et trois côtés. Par exemple, le triangle ABC comprend :
• Trois angles : \(\angle A\), \(\angle B\), \(\angle C\)
• Trois côtés : \([AB]\), \([AC]\), \([BC]\)
Le triangle rectangle
Un triangle rectangle est un triangle qui contient un angle de \(90°\).
Dans ce type de triangle, le côté qui fait face à l'angle droit porte le nom d'hypoténuse.
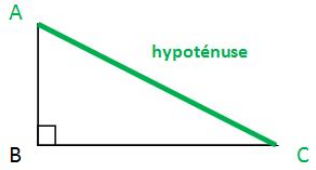
Le triangle ABC possède un angle droit en B. L'angle de \(90°\) se trouve en B, et \([AC]\) représente l'hypoténuse.
Le triangle isocèle
Un triangle isocèle est un triangle qui présente deux côtés de longueur identique.
Dans un triangle isocèle :
• L'angle formé par les deux côtés égaux s'appelle l'angle principal
• Le côté qui fait face à cet angle s'appelle la base
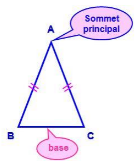
Le triangle ABC est isocèle en A. Les segments \([AB]\) et \([AC]\) ont la même longueur, A est l'angle principal et \([BC]\) constitue la base.
Le triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés ont exactement la même longueur.
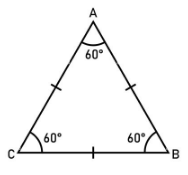
Un triangle équilatéral peut être considéré comme isocèle à partir de chacun de ses angles.
Classification complémentaire
• Triangle quelconque : Triangle qui ne présente aucune particularité (ni rectangle, ni isocèle, ni équilatéral)
• Triangle scalène : Triangle dont les trois côtés ont des longueurs toutes différentes
3) Les quadrilatères et leurs spécificités
Définition générale
Un quadrilatère est une figure géométrique composée de quatre segments de droite qui se connectent pour former une forme fermée.
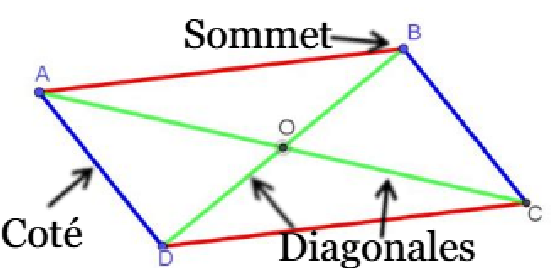
• Diagonales : Segments qui relient deux angles non adjacents
• Côtés opposés : Deux côtés qui ne partagent aucun angle commun (exemple : \([AD]\) et \([BC]\))
• Côtés adjacents : Deux côtés qui partagent un angle commun (exemple : \([AB]\) et \([BC]\))
Un quadrilatère se désigne en énumérant ses angles dans l'ordre (ABCD, DCBA, DABC, etc.). Il est interdit de sauter des angles (ACBD n'est pas acceptable).
Le rectangle
Un rectangle est un quadrilatère qui possède quatre angles de \(90°\).

• Les côtés qui se suivent sont perpendiculaires
• Les côtés qui se font face sont parallèles et de même longueur
Le losange
Un losange est un quadrilatère dont les quatre côtés ont la même longueur.
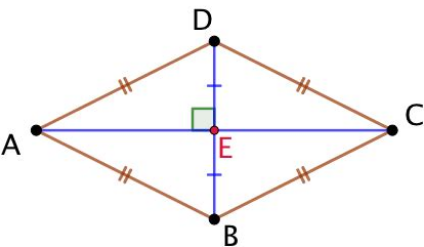
Les côtés opposés sont parallèles.
Le carré
Un carré est un quadrilatère qui combine quatre angles droits et quatre côtés de même longueur.
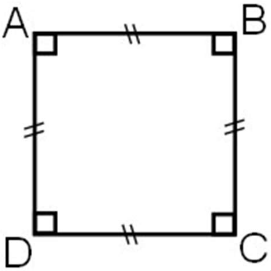
Un carré réunit les propriétés du rectangle et du losange.
Le parallélogramme
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
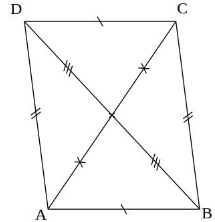
Dans le parallélogramme ABCD, on observe : \((AB) \parallel (CD)\) et \((AD) \parallel (BC)\)
Le rectangle, le losange et le carré sont des cas particuliers de parallélogrammes.
Relations entre les quadrilatères
Lien parallélogramme-rectangle :
Un rectangle est un parallélogramme qui possède un angle droit.
Un losange est un parallélogramme qui a deux côtés consécutifs de même longueur.
4) Utilisations concrètes
Applications dans la construction
• Créer des formes précises à l'aide d'outils géométriques
• Déterminer des périmètres et des surfaces
• Résoudre des problèmes géométriques complexes
Exemples d'usage dans la vie quotidienne
• Bâtiment : Les rectangles et carrés dominent l'architecture moderne
• Art : Les cercles et triangles créent des compositions visuelles équilibrées
• Ingénierie : Les quadrilatères constituent la base de nombreux systèmes techniques
Résumé
• Le cercle est défini par son centre et son rayon
• Les triangles se classent selon leurs angles et leurs côtés
• Les quadrilatères forment une famille hiérarchisée
• Les propriétés de ces figures permettent de résoudre des problèmes géométriques
• Les applications sont nombreuses dans la vie quotidienne