Proportionnalite
Sixieme
La Proportionnalité
Introduction
La proportionnalité est une relation mathématique fondamentale qui décrit comment deux grandeurs varient ensemble de manière prévisible. Cette notion est omniprésente dans notre vie quotidienne : prix des courses, vitesse de déplacement, recettes de cuisine... Comprendre la proportionnalité permet de résoudre de nombreux problèmes pratiques et de mieux appréhender le monde qui nous entoure.
1) Reconnaître une situation de proportionnalité
Définition fondamentale
Exemple concret : La quantité d'essence achetée et le prix payé sont proportionnels car, pour trouver le prix payé, on multiplie la quantité achetée par le prix d'un litre. Dans ce cas, le coefficient de proportionnalité est le prix d'un litre.
Le tableau de proportionnalité
Dans un tableau de proportionnalité, les nombres de la 2ème ligne peuvent être calculés en multipliant (ou en divisant) les nombres de la 1ère ligne par un même nombre. Ce nombre est appelé coefficient de proportionnalité.
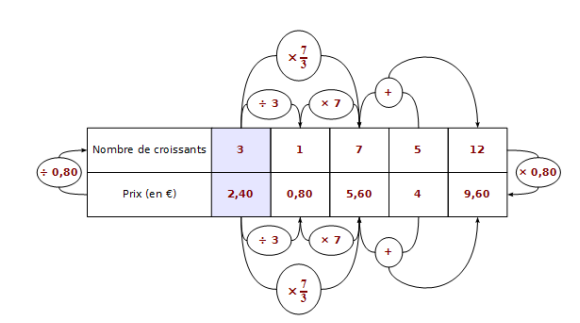
Exemple pratique : 3 croissants coûtent 2,40 €.
- Quel est le prix de 7 croissants ? de 5 croissants ?
- Quel nombre de croissants peut-on acheter avec 9,60 € ?
Le nombre de croissants et le prix sont proportionnels. On peut organiser les données et les calculs dans un tableau de proportionnalité.
2) Traiter une situation de proportionnalité
Méthode 1 : Utilisation de la propriété multiplicative
Principe : Quand deux grandeurs sont proportionnelles, si l'une est multipliée par un nombre, l'autre est multipliée par le même nombre.
Exemple : 5 bananes identiques pèsent 500 g. Calculer la masse de 20 bananes.
Raisonnement : Le nombre de bananes et la masse sont proportionnels. Or il y a 4 fois plus de bananes (20 ÷ 5 = 4). Donc la masse est 4 fois plus grande.
• 5 bananes → 500 g
• 20 bananes → ? g
Calcul : 4 × 500 g = 2000 g = 2 kg
Conclusion : Par conséquent, 20 bananes pèsent 2 kg.
Méthode 2 : Utilisation du passage à l'unité
Principe : On calcule d'abord la valeur correspondant à une unité, puis on multiplie par le nombre d'unités souhaité.
Exemple : Pour faire des crêpes pour 5 personnes, on a besoin de 400 g de farine, 3 œufs et 1 litre de lait. Quelle quantité de farine sera nécessaire pour 4 personnes ?
Raisonnement : Le nombre de personnes et la quantité de farine sont proportionnels. On calcule d'abord la quantité de farine nécessaire pour une personne.
Étape 1 : Calculer pour 1 personne
400 g ÷ 5 = 80 g de farine par personne
4 × 80 g = 320 g de farine
Conclusion : Par suite, il faut 320 g de farine pour faire des crêpes pour 4 personnes.
La règle de trois
On peut résumer ces étapes avec le calcul suivant : 400 × 4 ÷ 5, ce qu'on appelle la « règle de trois ».
| Farine (g) | 400 | ? |
| Personnes | 5 | 4 |
Formule : ? = 400 × 4 ÷ 5 = 320 g
Formule générale : Si a correspond à b, alors c correspond à (a × c) ÷ b
3) Utilisation de la propriété additive
Principe : Dans une situation de proportionnalité, si on additionne deux valeurs de la première grandeur, on additionne les valeurs correspondantes de la deuxième grandeur.
Exemple : À allure régulière, j'ai constaté que je parcours 18 km en 4 h. Quelle distance vais-je parcourir en 6 h ?
Raisonnement : À allure régulière, la distance parcourue et le temps sont proportionnels. Or 6 h = 4 h + 2 h. Et en 2 h, je parcours 9 km (2 fois moins qu'en 4 h).
Données :
• 4 h → 18 km
• 2 h → 9 km (moitié de 4 h, donc moitié de 18 km)
6 h = 4 h + 2 h
Distance = 18 km + 9 km = 27 km
Calcul : Donc en 6 h, je parcours 27 km (18 km + 9 km).
4) Utilisation du coefficient de proportionnalité
Principe : Le coefficient de proportionnalité est le nombre par lequel il faut multiplier les valeurs de la première grandeur pour obtenir les valeurs de la deuxième grandeur.

Exemple : Compléter le tableau de proportionnalité suivant :
| Durée de communications (h) | 3 | 7,5 | ? |
| Prix du forfait (€) | 35 | ? | 140 |
Raisonnement : Le prix du forfait et la durée de communications sont proportionnels. 3 ÷ 35 et 35 ÷ 3 ne donnent pas de valeur exacte. Exprimons alors le coefficient de proportionnalité sous une écriture fractionnaire : 35 ÷ 3 = $\frac{35}{3}$
Calcul : D'où : 7,5 × $\frac{35}{3}$ = (7,5 ÷ 3) × 35 = 2,5 × 35 = 87,5
Conclusion : Par conséquent, 7,5 h de communications coûtent 87,50 €.
5) Applications pratiques
Les pourcentages
Les pourcentages sont un cas particulier de proportionnalité où la deuxième grandeur est toujours 100.
Exemple : 15% de 200 = 200 × $\frac{15}{100}$ = 30
Les échelles
Une échelle est le coefficient de proportionnalité entre les dimensions réelles et les dimensions sur le plan.
Exemple : Une échelle de 1/1000 signifie que 1 cm sur le plan représente 1000 cm (soit 10 m) en réalité.
Les vitesses
La vitesse moyenne est le coefficient de proportionnalité entre la distance parcourue et le temps mis.
Formule : Vitesse = Distance ÷ Temps
Exemple : Si on parcourt 120 km en 2 h, la vitesse moyenne est de 60 km/h.
6) Méthodes de résolution
Résumé des méthodes
- Propriété multiplicative : Multiplier les deux grandeurs par le même nombre
- Passage à l'unité : Calculer la valeur pour 1 unité, puis multiplier
- Propriété additive : Additionner les valeurs correspondantes
- Coefficient de proportionnalité : Utiliser le rapport entre les grandeurs
- Règle de trois : Utiliser la formule (a × c) ÷ b
Conseils pratiques
- Toujours vérifier que les grandeurs sont bien proportionnelles
- Utiliser la méthode qui semble la plus simple pour chaque situation
- Faire un schéma ou un tableau pour organiser les données
- Vérifier la cohérence du résultat obtenu
Conclusion
La proportionnalité est un outil mathématique puissant qui permet de résoudre de nombreux problèmes de la vie quotidienne. Maîtriser ses différentes méthodes de résolution est essentiel pour aborder sereinement les mathématiques au collège et au-delà.