Dénombrement
Terminale
COURS: Dénombrement
Introduction
Le dénombrement est une branche des mathématiques qui s'intéresse au comptage d'objets ou d'arrangements selon certaines règles. Cette notion est fondamentale en probabilités, en statistiques et dans de nombreux domaines des mathématiques. Elle permet de calculer le nombre de possibilités dans des situations concrètes comme les jeux, les codes, les arrangements, etc.
I. Principes additif et multiplicatif
1. Principe additif : réunion d'ensembles disjoints
Soit \(E\) un ensemble fini. On appelle cardinal de \(E\), l'entier naturel noté \(\text{Card}(E)\) égal au nombre d'éléments de \(E\).
Soit \(E = \{-4; 15; -2; 0; 1,05; 3\}\). Alors \(\text{Card}(E) = 6\).
• Si \(E\) est l'ensemble vide, alors \(\text{Card}(E) = 0\)
• Certains ensembles ne sont pas finis : l'ensemble \(\mathbb{N}\) des entiers naturels, l'ensemble des réels de l'intervalle \([0;1]\) etc.
Soient \(E\) et \(F\) deux ensembles finis. On a alors :
\(\text{Card}(E \cup F) = \text{Card}(E) + \text{Card}(F) - \text{Card}(E \cap F)\)
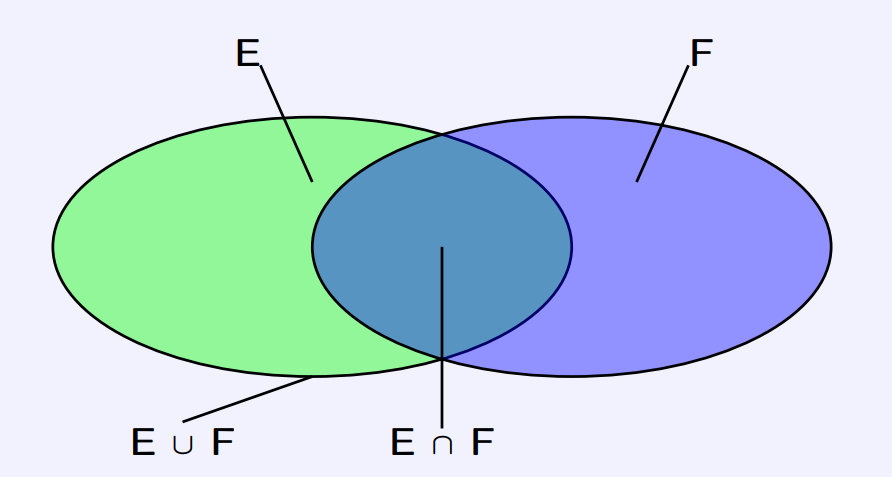
Soient \(E\) et \(F\) deux ensembles finis. On dit que \(E\) et \(F\) sont disjoints si et seulement si \(E \cap F = \emptyset\).
Soient \(E\) et \(F\) deux ensembles finis et disjoints. Alors :
\(\text{Card}(E \cup F) = \text{Card}(E) + \text{Card}(F)\)
On peut généraliser la propriété précédente dans le cas de \(n\) ensembles finis et deux à deux disjoints \(A_1, A_2, \ldots, A_n\) :
\(\text{Card}(A_1 \cup A_2 \cup \ldots \cup A_n) = \sum_{i=1}^{n} \text{Card}(A_i)\)
Soient \(E = \{a; b; c\}\) et \(F = \{d;e\}\).
- \(E\) et \(F\) sont-ils disjoints ? En déduire \(E \cap F\).
- Écrire \(E \cup F\) et préciser \(\text{Card}(E \cup F)\).
2. Principe multiplicatif : produit cartésien
Soient \(E\) et \(F\) deux ensembles non vides.
On appelle produit cartésien de \(E\) par \(F\) l'ensemble noté \(E \times F\) (« \(E\) croix \(F\) ») constitué des couples \((x;y)\), où \(x\) est un élément de \(E\) et \(y\) un élément de \(F\).
On le note \(E \times F = \{(x;y), x \in E \text{ et } y \in F\}\)
• On peut généraliser cette définition à plus de deux ensembles non vides
• Le produit cartésien de \(E\) par \(E\) est noté \(E^2\)
• \(\mathbb{R}^2\) pour les coordonnées d'un point du plan, \(\mathbb{R}^3\) pour celles d'un point de l'espace
• On lance deux dés : un dé à 6 faces numérotées de 1 à 6, et un dé à 4 faces colorées rouge, vert, bleu, jaune : \(D_1 = \{1;2;3;4;5;6\}\) et \(D_2 = \{\text{rouge}; \text{vert}; \text{bleu}; \text{jaune}\}\)
Un lancer possible est alors un élément de \(D_1 \times D_2\), par exemple \((4; \text{vert})\).
Soient \(E = \{a; b; c\}\) et \(F = \{1;2\}\). Déterminer l'ensemble \(E \times F\), puis l'ensemble \(F \times E\).
Soient \(E\) et \(F\) deux ensembles finis et non vides. Alors :
\(\text{Card}(E \times F) = \text{Card}(E) \times \text{Card}(F)\)
Chaque élément de \(E\) permet de générer autant de couples de \(E \times F\) que d'éléments de \(F\).
(Faire un arbre.) D'où le résultat.
II. k-uplets ou k-listes d'un ensemble
Soit \(E\) un ensemble non vide et \(k\) un entier naturel non nul.
On appelle k-uplet ou k-liste de \(E\) un élément de \(E^k\).
• Un 2-uplet est un couple et un 3-uplet est un triplet
• Un k-uplet de \(E\) est une liste ordonnée d'éléments de \(E\). Par exemple, le triplet \((1;2;3)\) n'est pas égal au triplet \((2;1;3)\)
• \((-2;3)\) est un couple d'éléments de \(\mathbb{R}\)
• \((\text{f};\text{u};\text{t};\text{u};\text{r})\) est un 5-uplet d'éléments de l'ensemble des 26 lettres \(E = \{\text{a};\text{b};\ldots; \text{z}\}\)
Soit \(E\) un ensemble fini non vide et \(k\) un entier naturel non nul. Alors :
\(\text{Card}(E^k) = \text{Card}(E)^k\)
Autrement dit, le nombre de k-uplets d'un ensemble \(E\) est \(\text{Card}(E)^k\).
Le digicode d'un immeuble est formé d'une lettre suivie de trois chiffres.
Combien y-a-t-il de codes possibles ?
III. Arrangements et permutations
1. Factorielle d'un entier naturel
Soit \(n\) un entier naturel non nul.
On appelle factorielle n, l'entier naturel noté \(n!\) (« factorielle n ») défini par :
\(n! = n \times (n-1) \times (n-2) \times \ldots \times 2 \times 1\)
Par convention, on admet que \(0! = 1\).
• Calculer \(4!\)
• Calculer astucieusement \(\frac{7!}{5!}\)
2. Arrangements d'un ensemble
Soit \(n\) un entier naturel non nul, \(E\) un ensemble fini non vide à \(n\) éléments, et \(k\) un entier naturel tel que \(0 \leq k \leq n\).
On appelle arrangement de \(k\) éléments de \(E\) tout k-uplet d'éléments distincts de \(E\).
• Si \(E = \{\text{a};\text{b};\text{c}\}\), alors les couples \((\text{a};\text{b})\) et \((\text{c};\text{a})\) sont deux arrangements possibles de 2 éléments de \(E\). Le couple \((\text{a};\text{a})\) n'est pas un arrangement car ses éléments ne sont pas distincts.
• Une course a lieu entre 20 concurrents. Le podium à l'arrivée de la course est un arrangement de 3 éléments de l'ensemble des 20 concurrents.
Soit \(n\) un entier naturel non nul et \(k\) un entier naturel tel que \(0 \leq k \leq n\).
Le nombre d'arrangements de \(k\) éléments parmi \(n\) est :
\(A_n^k = n \times (n-1) \times \ldots \times (n-k+1) = \frac{n!}{(n-k)!}\)
• Il y a \(n\) choix pour le premier élément de l'arrangement, puis \(n-1\) choix restants pour le deuxième élément de l'arrangement, et ainsi de suite, jusqu'à \(n-(k-1)\) choix restants pour le k-ième élément.
• \(\frac{n!}{(n-k)!} = \frac{n \times (n-1) \times \ldots \times (n-k+1) \times (n-k)!}{(n-k)!} = n \times (n-1) \times \ldots \times (n-k+1)\)
• Dans le premier exemple, il y a donc \(\frac{3!}{(3-2)!} = \frac{3 \times 2}{1} = 6\) arrangements possibles.
• Dans le 2ème exemple, il y a donc \(\frac{20!}{(20-3)!} = \frac{20 \times 19 \times 18 \times 17!}{17!} = 20 \times 19 \times 18 = 6840\) podiums possibles.
3. Permutations d'un ensemble
Soit \(n\) un entier naturel non nul et \(E\) un ensemble fini non vide à \(n\) éléments.
On appelle permutation de \(E\) tout n-uplet d'éléments distincts de \(E\).
Une permutation de \(E\) est donc un arrangement de \(n\) éléments de \(E\).
• Si \(E = \{\text{a};\text{b};\text{c}\}\), alors les triplets \((\text{a};\text{b};\text{c})\) et \((\text{b};\text{a};\text{c})\) sont deux (distinctes) permutations de \(E\).
• On considère un jeu de 32 cartes. Alors tout mélange de ce jeu est une permutation de l'ensemble des cartes du jeu.
Soit \(n\) un entier naturel non nul. Le nombre de permutations d'un ensemble à \(n\) éléments est \(n!\).
Il y a \(n\) choix pour le premier élément de la permutation, puis \(n-1\) choix restants pour le deuxième élément, et ainsi de suite, jusqu'à 1 choix restant pour le dernier élément.
• Dans le premier exemple, il y a donc \(3! = 3 \times 2 \times 1 = 6\) permutations possibles de \(E\).
• Dans le deuxième exemple, il y a donc \(32! \approx 2,6 \times 10^{35}\) mélanges de jeu possibles.
IV. Combinaisons
1. Parties d'un ensemble
Une partie d'un ensemble \(E\) est un sous-ensemble de \(E\), c'est-à-dire un ensemble constitué d'éléments de \(E\).
Si \(E = \{1;2;3;4;5;6\}\), alors les ensembles \(\{2;5\}\), \(\{3\}\), \(E\) et \(\emptyset\) sont des parties de \(E\).
Attention : ne pas confondre une partie d'un ensemble avec un k-uplet de cet ensemble.
Par exemple, \(\{1;2\}\) est une partie à deux éléments de l'ensemble \(\mathbb{N}\), et on a \(\{1;2\} = \{2;1\}\). En revanche, \((1;2)\) est un 2-uplet (couple) de l'ensemble \(\mathbb{N}\) et \((1;2) \neq (2;1)\).
Soit \(n\) un entier naturel et \(E\) un ensemble fini à \(n\) éléments. Alors le nombre de parties de \(E\) est \(2^n\).
Soit \(E'\) une partie de \(E\). Pour chaque élément de \(E\), il y a deux choix possibles : il est dans \(E'\), ou il ne l'est pas. Comme \(E\) possède \(n\) éléments, cela fait \(2^n\) possibilités pour créer \(E'\).
On peut visualiser cela avec un arbre de décision : pour chaque élément, on a deux branches (dans \(E'\) ou pas), ce qui donne \(2 \times 2 \times \ldots \times 2 = 2^n\) chemins possibles.
Ce résultat, \(2^n\), est égal au nombre de n-uplets de l'ensemble \(\{0;1\}\).
Par exemple, si \(E = \{1;2;3;4;5;6\}\), alors on peut faire correspondre la partie \(\{2;5\}\) au 6-uplet \((0;1;0;0;1;0)\).
2. Combinaisons
Soit \(n\) un entier naturel.
Soit \(E\) un ensemble fini à \(n\) éléments et soit \(k\) un entier naturel tel que \(0 \leq k \leq n\).
On appelle combinaison de \(k\) éléments de \(E\) toute partie de \(E\) à \(k\) éléments.
Le nombre de combinaison de \(k\) éléments parmi \(n\) est noté \(\binom{n}{k}\) et se lit « \(k\) parmi \(n\) ».
Soient \(n\) et \(k\) deux entiers naturels tels que \(0 \leq k \leq n\). Alors :
\(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)
Soit \(E\) un ensemble à \(n\) éléments.
\(\binom{n}{k}\) représente le nombre de parties de \(E\) constituées de \(k\) éléments parmi les \(n\) éléments de \(E\).
Or on a vu que le nombre de k-uplets d'éléments tous distincts de \(E\) est \(\frac{n!}{(n-k)!}\).
Pour obtenir un k-uplet d'éléments tous distincts de \(E\), il suffit d'abord de choisir une combinaison de \(k\) éléments de \(E\), puis de les ordonner.
Compter le nombre de façons d'ordonner \(k\) éléments revient à compter le nombre de permutations de \(k\) éléments : il y en a \(k!\)
Ainsi, on a \(\frac{n!}{(n-k)!} = \binom{n}{k} \times k!\)
Donc \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)
Au loto, on choisit 5 numéros entre 1 et 50. Combien y-a-t-il de tirages possibles ?
Il s'agit de compter le nombre de combinaisons possibles de 5 éléments parmi 50, soit \(\binom{50}{5}\) :
\(\binom{50}{5} = \frac{50!}{(50-5)! \times 5!} = \frac{50 \times 49 \times 48 \times 47 \times 46 \times 45!}{45! \times 5!} = \frac{50 \times 49 \times 48 \times 47 \times 46}{5 \times 4 \times 3 \times 2 \times 1} = 2\,118\,760\)
Il y a donc 2 118 760 tirages possibles au loto.
Pour gagner à l'Euromillions, il faut deviner les 5 bons numéros parmi 50 nombres, et les 2 étoiles gagnantes parmi 12 étoiles. Quelle est la probabilité de gagner le premier prix à l'Euromillions ?
Réponse : 139 838 160 tirages possibles, soit une probabilité de gagner de \(7,15 \times 10^{-9}\).
3. Propriétés des combinaisons
Soient \(n\) et \(k\) deux entiers naturels tels que \(0 \leq k \leq n\). Alors :
• \(\binom{n}{k} = \binom{n}{n-k}\) (symétrie)
• \(\binom{n}{0} = 1\)
• \(\binom{n}{1} = n\) et \(\binom{n}{n} = 1\)
• Relation de Pascal : \(\binom{n}{k} + \binom{n}{k+1} = \binom{n+1}{k+1}\)
On utilise la formule \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) pour obtenir ces résultats :
• \(\binom{n}{n-k} = \frac{n!}{(n-k)!(n-(n-k))!} = \frac{n!}{(n-k)!k!} = \frac{n!}{k!(n-k)!} = \binom{n}{k}\)
• \(\binom{n}{0} = \frac{n!}{0!(n-0)!} = \frac{n!}{1 \times n!} = \frac{n!}{n!} = 1\)
• \(\binom{n}{1} = \frac{n!}{1!(n-1)!} = \frac{n!}{1 \times (n-1)!} = \frac{n \times (n-1)!}{(n-1)!} = n\)
• Pour la relation de Pascal : \(\binom{n}{k} + \binom{n}{k+1} = \frac{n!}{k!(n-k)!} + \frac{n!}{(k+1)!(n-(k+1))!} = \frac{n!(k+1)}{(k+1)!(n-k)!} + \frac{n!(n-k)}{(k+1)!(n-k)!} = \frac{n!(k+1+n-k)}{(k+1)!(n-k)!} = \frac{n!(n+1)}{(k+1)!(n-k)!} = \frac{(n+1)!}{(k+1)!(n-k)!} = \frac{(n+1)!}{(k+1)!(n+1-(k+1))!} = \binom{n+1}{k+1}\)
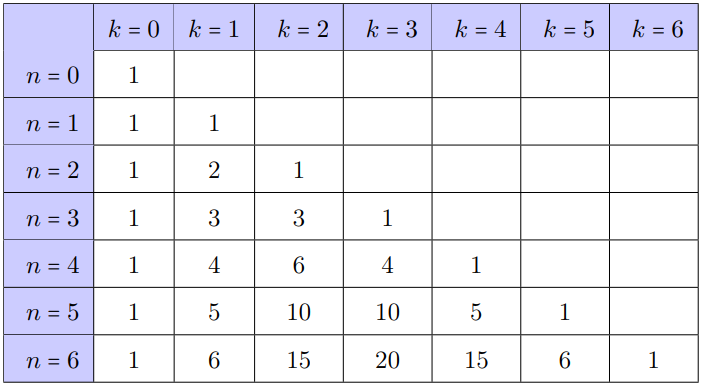
4. Triangle de Pascal
Le triangle de Pascal permet d'obtenir rapidement les valeurs de \(\binom{n}{k}\) pour les premières valeurs de \(k\) et de \(n\).
Pour tous réels \(a\) et \(b\) et pour tout entier naturel \(n\) non nul, on a :
\((a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k\)
La formule ainsi obtenue est appelée la formule du binôme de Newton et les entiers \(\binom{n}{k}\) sont appelés les coefficients binomiaux.
Cette formule se démontre en Maths Expertes.
Soit \(n \in \mathbb{N}^*\) et soit \(k \in \mathbb{N}\) tel que \(0 \leq k \leq n\). Alors :
\(\sum_{k=0}^{n} \binom{n}{k} = 2^n\)
On peut conjecturer ce résultat à partir du triangle de Pascal en additionnant pour chaque ligne les nombres qui la composent.
Soit \(E\) un ensemble fini à \(n\) éléments.
Par définition, \(\binom{n}{k}\) est le nombre de combinaisons de \(k\) éléments de \(E\), autrement dit le nombre de parties de \(E\) ayant \(k\) éléments.
Ainsi, d'après le principe additif, \(\sum_{k=0}^{n} \binom{n}{k}\) est le nombre total de parties de \(E\).
Or il y a \(2^n\) parties de \(E\) (propriété précédemment démontrée), donc on a bien \(\sum_{k=0}^{n} \binom{n}{k} = 2^n\).
Exercices d'application
Un restaurant propose un menu avec 3 entrées, 4 plats principaux et 2 desserts.
1) Combien de menus différents peut-on composer ?
2) Si on ne veut pas prendre d'entrée, combien de menus peut-on composer ?
3) Si on veut exactement 2 éléments (parmi entrée, plat, dessert), combien de choix avons-nous ?
Dans une classe de 30 élèves, on veut former une équipe de 5 élèves pour représenter la classe.
1) Combien d'équipes différentes peut-on former ?
2) Si 2 élèves ne peuvent pas être dans la même équipe, combien d'équipes peut-on former ?
3) Si on veut que l'équipe contienne exactement 3 filles et 2 garçons, et qu'il y a 18 filles dans la classe, combien d'équipes peut-on former ?
On dispose de 8 couleurs différentes pour peindre les 6 faces d'un cube.
1) Combien de façons différentes peut-on peindre le cube si chaque face doit avoir une couleur différente ?
2) Combien de façons différentes peut-on peindre le cube si on peut utiliser plusieurs fois la même couleur ?
3) Combien de façons différentes peut-on peindre le cube si exactement 2 faces doivent avoir la même couleur ?
Résumé
• Principe additif : \(\text{Card}(E \cup F) = \text{Card}(E) + \text{Card}(F) - \text{Card}(E \cap F)\)
• Principe multiplicatif : \(\text{Card}(E \times F) = \text{Card}(E) \times \text{Card}(F)\)
• k-uplets : \(\text{Card}(E^k) = \text{Card}(E)^k\)
• Factorielle : \(n! = n \times (n-1) \times \ldots \times 2 \times 1\) avec \(0! = 1\)
• Arrangements : \(A_n^k = \frac{n!}{(n-k)!}\)
• Permutations : \(n!\) pour un ensemble à \(n\) éléments
• Combinaisons : \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)
• Parties d'un ensemble : \(2^n\) pour un ensemble à \(n\) éléments
• Triangle de Pascal : \(\binom{n}{k} + \binom{n}{k+1} = \binom{n+1}{k+1}\)
• Formule du binôme : \((a+b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k\)