Soit \(n\) expériences aléatoires indépendantes.

Chaque expérience \(i\) est modélisée par une probabilité \(P_i\) sur son univers \(\Omega_i\).

Cette succession peut être considérée comme une seule expérience aléatoire sur l'univers \(\Omega = \Omega_1 \times \Omega_2 \times \ldots \times \Omega_n\).

Un résultat de cette expérience est un \(n\)-uplet \((x_1, x_2, \ldots, x_n)\) où \(x_i\) est un résultat de \(\Omega_i\).

La probabilité \(P\) d'un tel \(n\)-uplet est définie par : \(P((x_1, x_2, \ldots, x_n)) = P_1(x_1) \times P_2(x_2) \times \ldots \times P_n(x_n)\).

Un jeu consiste à :

• Lancer un dé à 6 faces

• Tirer une carte dans un jeu de 32 cartes

• Lancer une pièce

Ces trois expériences sont indépendantes.

La probabilité \(p\) d'obtenir un six, un as et pile est :

\(p = \frac{1}{6} \times \frac{4}{32} \times \frac{1}{2} = \frac{1}{96}\)

Dans le jeu précédent, on gagne :

• 1 point si on obtient un six

• 1 point si on obtient un as

• 1 point si on obtient pile

Soit \(X\) la variable aléatoire donnant le nombre de points obtenus.

1) Déterminer la loi de probabilité de \(X\).

2) Calculer l'espérance et la variance de \(X\).

Une expérience de Bernoulli de paramètre \(p\) est une expérience aléatoire ayant exactement deux issues :

• Le succès (noté \(S\)), avec une probabilité \(p(S) = p\)

• L'échec (noté \(\overline{S}\)), avec une probabilité \(p(\overline{S}) = 1-p\)

Une urne contient 10 boules : 7 sont rouges et 3 sont bleues.

Un joueur tire une boule au hasard dans l'urne.

On note succès l'événement : "la boule est rouge".

On a donc \(p(S) = \frac{7}{10} = 0,7\)

Et \(p(\overline{S}) = \frac{3}{10} = 0,3\)

Soit une expérience de Bernoulli de paramètre \(p\) et \(X\) la variable aléatoire prenant la valeur 1 en cas de succès et la valeur 0 en cas d'échec.

La loi de probabilité de \(X\) est appelée loi de Bernoulli de paramètre \(p\).

Si la variable aléatoire \(X\) suit une loi de Bernoulli de paramètre \(p\), alors :

• Espérance : \(E(X) = p\)

• Variance : \(V(X) = p(1-p)\)

• Écart-type : \(\sigma(X) = \sqrt{p(1-p)}\)

Lorsqu'on répète \(n\) fois, dans des conditions identiques et indépendantes, une même expérience de Bernoulli de paramètre \(p\), alors la loi de probabilité de la variable aléatoire \(X\) qui associe le nombre de succès obtenus au bout des \(n\) répétitions est appelée loi binomiale de paramètres \(n\) et \(p\).

On note alors : \(X \sim \mathcal{B}(n,p)\)

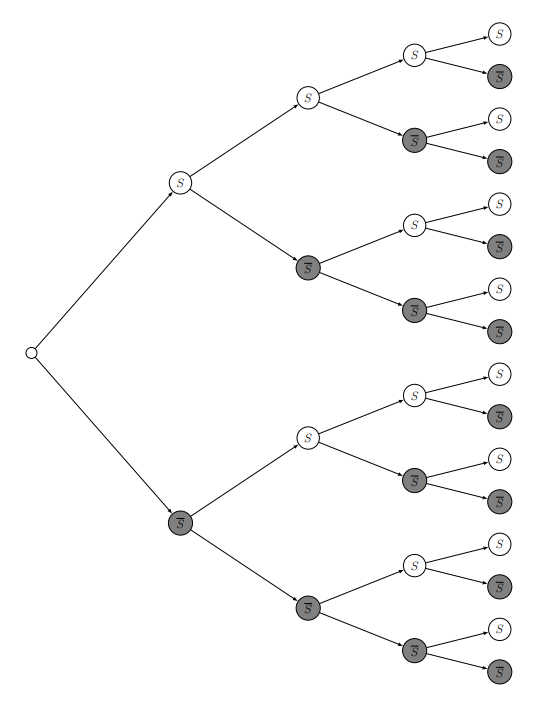
L'arbre ci-dessus représente 4 épreuves de Bernoulli indépendantes. Chaque chemin de la racine vers une feuille représente une suite possible de résultats. Il y a \(2^4 = 16\) chemins possibles au total.

Si \(X \sim \mathcal{B}(n,p)\), alors pour tout entier \(k\) entre 0 et \(n\) :

\(P(X = k) = \binom{n}{k} \times p^k \times (1-p)^{n-k}\)

Pour une urne contenant 7 boules rouges et 3 boules bleues.

Le joueur décide de tirer 5 fois consécutivement, en remettant la boule dans l'urne à chaque tirage.

Soit \(X\) la variable aléatoire associant le nombre de boules rouges obtenues au bout des 5 tirages.

On a donc : \(X \sim \mathcal{B}(5, 0,7)\)

La probabilité d'obtenir exactement 3 boules rouges est :

\(P(X = 3) = \binom{5}{3} \times 0,7^3 \times 0,3^2 = 10 \times 0,343 \times 0,09 = 0,3087\)

Si \(X \sim \mathcal{B}(n,p)\), alors :

• Espérance : \(E(X) = np\)

• Variance : \(V(X) = np(1-p)\)

• Écart-type : \(\sigma(X) = \sqrt{np(1-p)}\)

\(X\) peut s'écrire comme la somme de \(n\) variables de Bernoulli indépendantes \(X_1, X_2, \ldots, X_n\) de paramètre \(p\).

Donc : \(X = X_1 + X_2 + \ldots + X_n\)

Par linéarité de l'espérance : \(E(X) = E(X_1) + E(X_2) + \ldots + E(X_n) = p + p + \ldots + p = np\)

Calculer les probabilités \(P(X=k)\) et \(P(X \leq k)\) où \(X \sim \mathcal{B}(10; 0,4)\).

• Taper sur OPT puis STAT puis DIST puis BINOMIAL

• Pour calculer \(P(X=6)\) : choisir Bpd puis saisir BinomialPD(6,10,0.4)

• Pour calculer \(P(X \leq 3)\) : choisir Bcd puis saisir BinomialCD(3,10,0.4)

• Taper 2nd puis VAR (pour avoir DISTRIB)

• Pour calculer \(P(X=6)\) : rechercher binomFdp puis saisir binomFdp(10,0.4,6)

• Pour calculer \(P(X \leq 3)\) : sélectionner binomFRép puis saisir binomFRép(10,0.4,3)

Soient \(n\) un entier naturel non nul, \(\alpha\) et \(p\) des réels appartenant à \([0;1]\) et \(X\) une variable aléatoire qui suit la loi binomiale \(\mathcal{B}(n,p)\).

Il existe un intervalle \(I\) non vide tel que \(P(X \in I) \geq 1-\alpha\).

Pour déterminer un intervalle \(I\) pour lequel \(P(X \in I)\) est supérieure ou égale à une valeur donnée, on peut construire avec une calculatrice une table des valeurs \(P(X \leq k)\).

Construire le tableau des valeurs \(P(X \leq k)\) où \(X \sim \mathcal{B}(15, 0,3)\) :

• Taper MENU puis TABL

• Dans Y1, saisir BinomialCD(X,15,0.3)

• Taper sur SET puis : Start : 0, End : 15, Step : 1

• Taper sur TABL

• Taper sur f(x)

• Dans Y1, saisir BinomFRép(15,0.3,X)

• Taper sur def table : DebutTbl : 0, ΔTbl : 1

• Taper table

On s'intéresse à la proportion de faces marquées 1 obtenues quand on lance un dé tétraédrique bien équilibré (dont les faces sont numérotées de 1 à 4).

Soit \(Y\) la variable aléatoire qui, à chaque série de 100 lancers, associe le nombre de 1 obtenus.


1) Déterminer la loi de \(Y\).

2) Déterminer les entiers \(a\) et \(b\) tels que \(a\) est le plus petit entier tel que \(P(Y \leq a) > 0,025\) et \(b\) est le plus petit entier tel que \(P(Y \leq b) \geq 0,975\).

3) En déduire un intervalle \(I\) tel que \(P(Y \in I) \geq 0,95\) et interpréter ce résultat.

Dans une population, 60% des personnes préfèrent le chocolat noir au chocolat blanc.

On interroge 20 personnes au hasard dans cette population.

Soit \(X\) la variable aléatoire donnant le nombre de personnes préférant le chocolat noir.


1) Justifier que \(X\) suit une loi binomiale et préciser ses paramètres.

2) Calculer la probabilité qu'exactement 12 personnes préfèrent le chocolat noir.

3) Calculer la probabilité qu'au moins 15 personnes préfèrent le chocolat noir.

4) Calculer l'espérance et l'écart-type de \(X\).

• Loi de Bernoulli : Une expérience à deux issues (succès/échec)

• Loi binomiale : Répétition de \(n\) épreuves de Bernoulli indépendantes

• Notation : \(X \sim \mathcal{B}(n,p)\) où \(n\) = nombre d'épreuves, \(p\) = probabilité de succès

• Formule : \(P(X = k) = \binom{n}{k} \times p^k \times (1-p)^{n-k}\)

• Espérance : \(E(X) = np\)

• Variance : \(V(X) = np(1-p)\)

• Calculatrice : Bpd/BinomialPD pour \(P(X=k)\), Bcd/BinomialCD pour \(P(X \leq k)\)

• Échantillonnage : Construction d'intervalles de fluctuation