Divisions
Sixieme
La Division
Introduction
La division est une opération mathématique fondamentale qui permet de partager une quantité en parts égales. Elle est omniprésente dans notre vie quotidienne : partager des bonbons entre amis, calculer le prix unitaire d'un produit, déterminer une vitesse moyenne... Maîtriser la division est essentiel pour résoudre de nombreux problèmes pratiques.
I. Divisibilité
1. Définitions fondamentales
Un nombre entier \(a\) est divisible par un nombre entier \(b\) (non nul) s'il existe un nombre entier \(q\) tel que \(a = b \times q\).
\(56 = 8 \times 7\)
• \(7\) et \(8\) sont des diviseurs de \(56\)
• On dit aussi : \(56\) est divisible par \(7\) et par \(8\)
• \(56\) est un multiple de \(7\) et de \(8\)
2. Critères de divisibilité
Divisibilité par 2
Un nombre est divisible par 2, s'il est pair (il se termine par 0, 2, 4, 6 ou 8).
• \(26\) est divisible par 2 (se termine par 6)
• \(48\) est divisible par 2 (se termine par 8)
• \(10\,024\) est divisible par 2 (se termine par 4)
Divisibilité par 5
Un nombre est divisible par 5, s'il se termine par 0 ou 5.
• \(855\) est divisible par 5 (se termine par 5)
• \(1\,250\) est divisible par 5 (se termine par 0)
Divisibilité par 10
Un nombre est divisible par 10, s'il se termine par 0.
• \(2\,150\) est divisible par 10 (se termine par 0)
• \(548\,950\) est divisible par 10 (se termine par 0)
Divisibilité par 3
Un nombre est divisible par 3, si la somme de ses chiffres est divisible par 3.
\(532\,587\) (car \(5+3+2+5+8+7=30\) et \(30\) est divisible par 3)
Divisibilité par 9
Un nombre est divisible par 9, si la somme de ses chiffres est divisible par 9.
\(73\,854\) (car \(7+3+8+5+4=27\) et \(27\) est divisible par 9)
II. La Division
1. La division euclidienne
C'est une division faisant intervenir uniquement des nombres entiers.
Méthode de la division euclidienne
Étape 1 :
Dans \(73\), combien de fois \(34\) ? \(2\) fois !
\(2 \times 34 = 68\)
\(73 - 68 = 5\) (inférieur au diviseur)
On abaisse le \(1\) → \(51\)
Dans \(51\), combien de fois \(34\) ? \(1\) fois !
\(1 \times 34 = 34\)
\(51 - 34 = 17\) (inférieur au diviseur)
On arrête, il n'y a plus rien à abaisser.
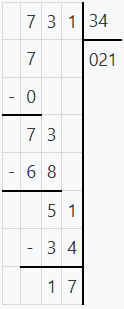
• Dividende : \(731\)
• Diviseur : \(34\)
• Quotient : \(21\)
• Reste : \(17\)
Le reste est toujours inférieur au diviseur.
Formule générale :
DIVIDENDE = DIVISEUR × QUOTIENT + RESTE
On ne peut pas diviser par zéro !
2. La division décimale
La division décimale permet d'obtenir un quotient décimal exact ou approché.
Méthode de la division décimale
Lorsqu'on franchit la virgule (,) au dividende, on la franchit aussi au quotient.

Étapes :
• \(45 \div 8 = 5\) reste \(5\)
• On ajoute un \(0\) → \(50 \div 8 = 6\) reste \(2\)
• On ajoute un \(0\) → \(20 \div 8 = 2\) reste \(4\)
• On ajoute un \(0\) → \(40 \div 8 = 5\) reste \(0\)

Étapes :
• \(32 \div 4 = 8\) reste \(0\)
• On abaisse le \(1\) → \(1 \div 4 = 0\) reste \(1\)
• On abaisse le \(2\) → \(12 \div 4 = 3\) reste \(0\)
III. Applications pratiques
Dans la vie quotidienne
• Partage : Répartir \(24\) bonbons entre \(6\) enfants
• Prix unitaire : Calculer le prix d'un article si \(3\) coûtent \(15\)€
• Vitesse : Calculer la vitesse moyenne sur \(120\) km en \(2\) heures
• Proportions : Adapter une recette pour \(4\) personnes au lieu de \(6\)
En géométrie
• Périmètre : Calculer le côté d'un carré de périmètre \(20\) cm
• Aire : Calculer la largeur d'un rectangle d'aire \(24\) cm² et de longueur \(6\) cm
• Volume : Calculer la hauteur d'un prisme de volume \(60\) cm³ et d'aire de base \(12\) cm²
IV. Méthodes de vérification
Vérification par multiplication
Pour vérifier une division, on multiplie le quotient par le diviseur et on ajoute le reste.
Vérification : \(34 \times 21 + 17 = 714 + 17 = 731\) ✓
Vérification par estimation
Estimer le résultat pour vérifier la cohérence.
• \(34 \times 20 = 680\)
• \(34 \times 30 = 1020\)
• Le quotient doit être entre \(20\) et \(30\) ✓
Résumé
• La divisibilité permet de reconnaître les multiples d'un nombre
• La division euclidienne donne un quotient entier et un reste
• La division décimale donne un quotient décimal exact ou approché
• Le reste est toujours inférieur au diviseur
• La vérification se fait par multiplication
• On ne peut jamais diviser par zéro
Exercices d'application
- Effectuer la division euclidienne de \(847\) par \(23\)
- Calculer \(156,8 \div 4\)
- Vérifier si \(2\,847\) est divisible par \(3\)
- Calculer le prix unitaire de \(5\) articles coûtant \(37,50\)€
- Partager \(180\)€ entre \(12\) personnes
- Calculer la vitesse moyenne d'un véhicule parcourant \(240\) km en \(3\) heures