Grandeurs Périmetres Et Aires
Sixieme
Grandeurs et Mesures
Introduction
Les grandeurs et mesures sont des concepts fondamentaux en mathématiques qui nous permettent de quantifier le monde qui nous entoure. Ce cours vous permettra de comprendre les unités de mesure, les conversions et les calculs de périmètres et d'aires.
I. Grandeurs usuelles
Définition
• Pour mesurer les longueurs, on utilise une longueur de référence appelée mètre, notée m
• Pour mesurer les masses, on utilise une masse de référence appelée gramme, notée g
• Pour mesurer le temps, on utilise une durée de référence appelée seconde, notée s
Principe de base
Certaines distances peuvent être mesurées en mètres : la distance entre deux élèves dans une salle de classe, la taille d'un élève... Pour des distances un peu plus grandes, on peut utiliser un mètre ruban ou un télémètre laser.
Quand les distances sont trop grandes (entre deux villes, entre deux planètes) ou trop petites (distance entre deux points A et B, taille d'un microbe), il faut utiliser d'autres unités plus adaptées.
Les conversions d'unités
Comme pour la numération, on fait des paquets de 10 unités ou on découpe en 10 parties égales. On peut utiliser les tableaux suivants :
10 mètres donnent 1 décamètre, 10 décamètres donnent 1 hectomètre...
10 grammes donnent 1 décagramme, 10 décagrammes donnent 1 hectogramme...
Ce principe de base ne fonctionne pas pour le temps. En effet, les secondes ne sont pas rangées par 10, mais par 60. 60 secondes donnent 1 minute, 60 minutes donnent 1 heure, 24 heures donnent 1 journée...
• 1 km = 10 hm = 100 dam = 1000 m et 1 m = 10 dm = 100 cm = 1000 mm
• 1 kg = 10 hg = 100 dag = 1000 g et 1 g = 10 dg = 100 cg = 1000 mg
II. Périmètre d'une figure
Définition générale
La longueur de la distance du contour d'une figure est appelée le périmètre de la figure.
1. Périmètre d'un polygone
Définition générale : Le périmètre d'un polygone est la somme des longueurs de tous ses côtés.
Exemple : Calculer le périmètre du polygone ABCDEF suivant :
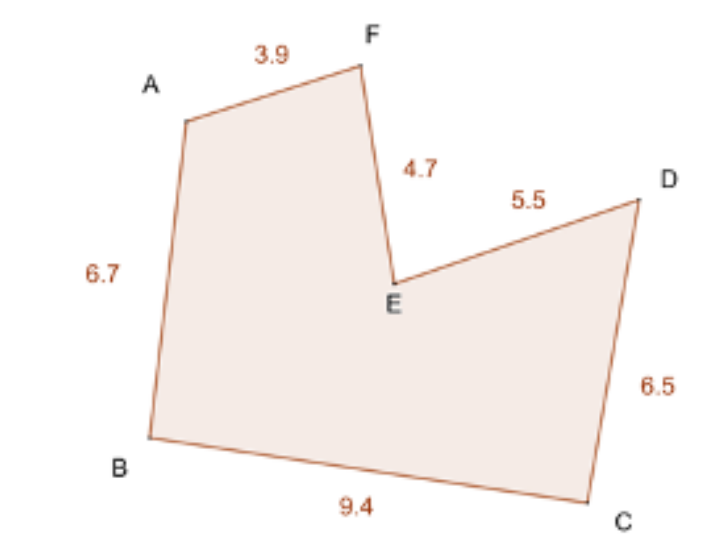
• AB = 6,7 cm
• BC = 9,4 cm
• CD = 6,5 cm
• DE = 5,5 cm
• EF = 4,7 cm
• FA = 3,9 cm
Formule : \(P = AB + BC + CD + DE + EF + FA\)
Application : \(P = 6,7 + 9,4 + 6,5 + 5,5 + 4,7 + 3,9\)
Résultat : \(P = 36,7 \text{ cm}\)
Conclusion : Le périmètre du polygone ABCDEF est de 36,7 cm.
Polygones usuels
Pour les polygones usuels, il est utile de connaître des formules permettant un calcul rapide du périmètre.
On note en abrégé les mots « longueurs », « largeur » et « côté ».
• Le mot « longueur » sera noté L
• Le mot « largeur » sera noté l
• Le mot « côté » sera noté c
Rectangle :
• \(P = L + L + l + l\)
• ou alors \(P = 2 \times L + 2 \times l\)
• \(P = c + c + c + c\)
• ou alors \(P = 4 \times c\)
• \(P = c + c + c + c\)
• ou alors \(P = 4 \times c\)
2. Périmètre d'un cercle
Pour un cercle, c'est assez difficile de placer la règle tout autour. On utilise alors la formule suivante :
La longueur du contour d'un cercle est donnée par la formule :
Exemple : Voici un cercle de rayon 4,1 cm.
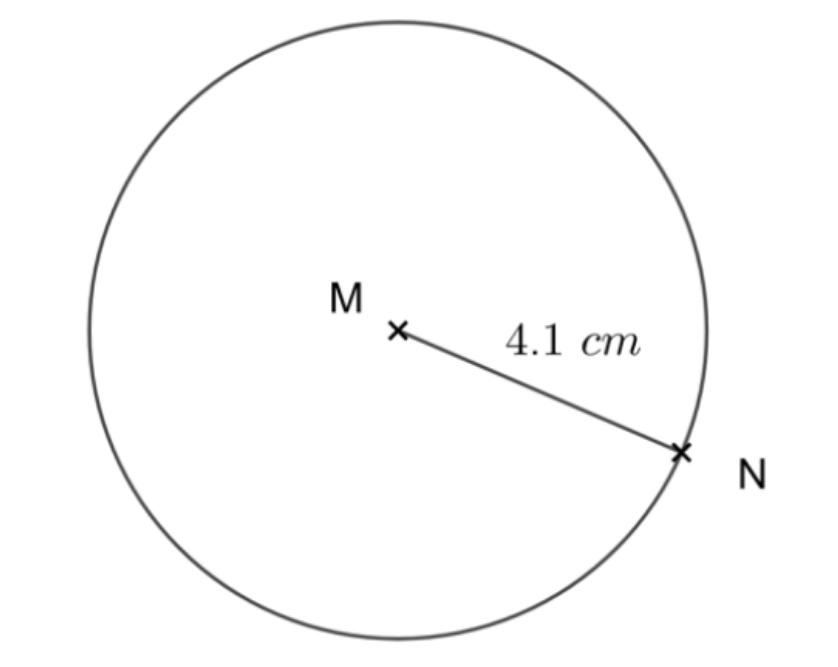
Formule : \(P = \pi \times \text{diamètre}\)
Calcul : \(P = \pi \times (4,1 \times 2) = \pi \times 8,2\)
Résultat : \(P \approx 25,8 \text{ cm}\)
Conclusion : Le périmètre du cercle est de 25,8 cm.
• On utilise la calculatrice pour effectuer le calcul.
• On a multiplié par 2 dans le calcul précédent car on ne connaissait pas la longueur diamètre mais la longueur du rayon.
III. Aire d'une figure
1. Généralités
L'aire d'une figure est la mesure de sa surface.
• On dit souvent que l'aire d'une figure est « l'intérieur » de la figure.
• L'aire d'une figure se mesure à l'aide d'une unité de mesure, appelée unité d'aire. Il s'agit d'un carré de 1 unité de côté. Cette unité de mesure dépend de la taille de la figure dont on veut mesurer l'aire. Par exemple :
• pour une pièce (salle de classe, chambre, réfectoire...) : on utilise un carré de côté 1 m : le mètre carré noté m²
• pour une figure sur une feuille du cahier (dans un exercice...) : on utilise un carré de côté 1 cm : le centimètre carré noté cm²
• pour une ville (Paris, New-York, Tokyo, Dax...) : on utilise un carré de côté 1 km : le kilomètre carré noté km²
Méthode par comptage
Exemple : Pour la figure suivante, on se demande : « Combien de carrés 'unité d'aire' faut-il pour remplir la figure ABCDEFG ? »
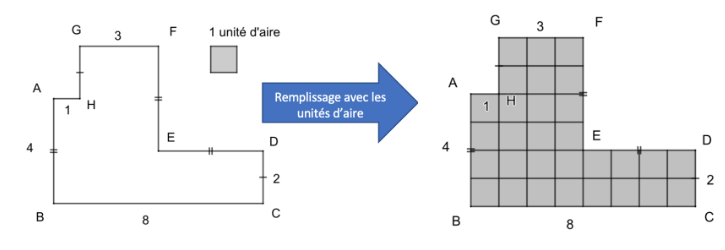
• Forme en L avec les dimensions suivantes :
• AB = 4 unités (hauteur)
• BC = 8 unités (largeur)
• CD = 2 unités (hauteur)
• DE = 5 unités (largeur)
• EF = 2 unités (hauteur)
• FG = 3 unités (largeur)
• GA = 4 unités (hauteur)
Résultat : Après comptage, on trouve 28 unités d'aire dans la figure ABCDEFG.
Cette stratégie peut s'avérer longue et inefficace. Que se passe-t-il si la figure ne comporte pas d'angles droits ? ou comporte des arrondis ? Il nous faut une autre stratégie...
2. Formules usuelles
Comme pour les périmètres, on fait un tableau avec les figures usuelles.
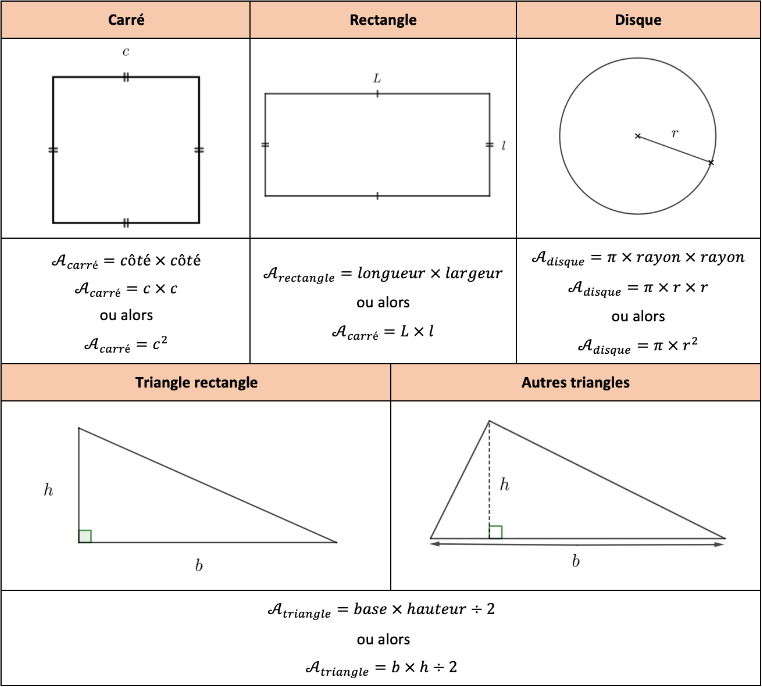
Carré :
• \(A_{\text{carré}} = \text{côté} \times \text{côté}\)
• \(A_{\text{carré}} = c \times c\)
• ou alors \(A_{\text{carré}} = c^2\)
• \(A_{\text{rectangle}} = \text{longueur} \times \text{largeur}\)
• ou alors \(A_{\text{rectangle}} = L \times l\)
• \(A_{\text{disque}} = \pi \times \text{rayon} \times \text{rayon}\)
• \(A_{\text{disque}} = \pi \times r \times r\)
• ou alors \(A_{\text{disque}} = \pi \times r^2\)
• \(A_{\text{triangle}} = \text{base} \times \text{hauteur} \div 2\)
• ou alors \(A_{\text{triangle}} = b \times h \div 2\)
• \(A_{\text{triangle}} = \text{base} \times \text{hauteur} \div 2\)
• ou alors \(A_{\text{triangle}} = b \times h \div 2\)
Conclusion
Les grandeurs et mesures sont essentielles pour comprendre et quantifier le monde qui nous entoure. Maîtriser les unités de mesure, les conversions, les calculs de périmètres et d'aires vous permettra de résoudre de nombreux problèmes pratiques dans la vie quotidienne et dans vos études mathématiques.