Solides Et Volumes
Sixieme
Les Solides et les Volumes
Introduction
Les solides sont des figures géométriques en trois dimensions qui occupent un espace. Comprendre les différents types de solides et savoir calculer leur volume est essentiel pour résoudre de nombreux problèmes pratiques : calculer la capacité d'un réservoir, déterminer la quantité de matériau nécessaire pour construire un objet, ou encore estimer l'espace occupé par un meuble.
I. Les différents types de solides
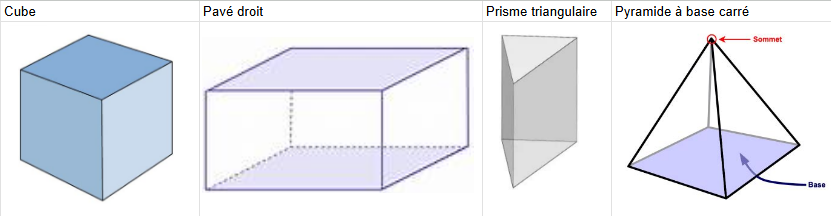
1. Les polyèdres
Un polyèdre est un solide dont toutes les faces sont des polygones (figures planes à plusieurs côtés).
Les prismes
• Deux bases parallèles et identiques
• Faces latérales rectangulaires
• Arêtes parallèles entre les bases
• Pavé droit (parallélépipède rectangle) : Prisme à base rectangulaire
• Cube : Prisme à base carrée avec toutes les arêtes égales
• Prisme triangulaire : Prisme à base triangulaire
• Prisme hexagonal : Prisme à base hexagonale
Les pyramides
• Une base polygonale
• Un sommet (apex) qui n'appartient pas à la base
• Faces latérales triangulaires
• Pyramide à base carrée : Base carrée, 4 faces triangulaires
• Pyramide à base triangulaire (tétraèdre) : Base triangulaire, 3 faces triangulaires
• Pyramide à base hexagonale : Base hexagonale, 6 faces triangulaires
2. Les solides de révolution
Un solide de révolution est obtenu en faisant tourner une figure plane autour d'un axe.
Le cylindre
• Deux bases circulaires parallèles et identiques
• Surface latérale courbe (rectangle enroulé)
• Hauteur perpendiculaire aux bases
Le cône
• Une base circulaire
• Un sommet (apex) qui n'appartient pas à la base
• Surface latérale courbe
La sphère
• Surface entièrement courbe
• Tous les points de la surface sont à égale distance du centre
• Pas de faces, d'arêtes ni de sommets
II. Le volume des solides
1. Définition du volume
Le volume d'un solide est la mesure de l'espace qu'il occupe dans l'espace à trois dimensions.
• Unité de base : Le mètre cube (m³)
• Multiples : km³, hm³, dam³
• Sous-multiples : dm³, cm³, mm³
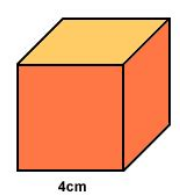
2. Volume du cube
\(V_{cube} = c \times c \times c = c^3\)
où \(c\) est la longueur d'une arête du cube
Un cube d'arête \(4\) cm a un volume de :
\(V = 4 \times 4 \times 4 = 64\) cm³
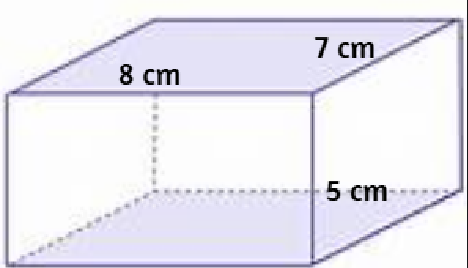
3. Volume du pavé droit (parallélépipède rectangle)
\(V_{pavé} = L \times l \times h\)
où \(L\) est la longueur, \(l\) la largeur et \(h\) la hauteur
Un pavé droit de dimensions \(8\) cm × \(5\) cm × \(3\) cm a un volume de :
\(V = 8 \times 5 \times 3 = 120\) cm³
4. Volume du cylindre
\(V_{cylindre} = \pi \times r^2 \times h\)
où \(r\) est le rayon de la base et \(h\) la hauteur
Un cylindre de rayon \(3\) cm et de hauteur \(7\) cm a un volume de :
\(V = \pi \times 3^2 \times 7 = \pi \times 9 \times 7 = 63\pi\) cm³ ≈ \(198\) cm³
5. Volume de la sphère
\(V_{sphère} = \frac{4}{3} \times \pi \times r^3\)
où \(r\) est le rayon de la sphère
Une sphère de rayon \(5\) cm a un volume de :
\(V = \frac{4}{3} \times \pi \times 5^3 = \frac{4}{3} \times \pi \times 125 = \frac{500}{3}\pi\) cm³ ≈ \(524\) cm³
III. Les unités de volume et de contenance
1. Les unités de volume
Les unités de volume mesurent l'espace occupé par un solide. L'unité de référence est le mètre cube (m³).
10 mètres cubes donnent 1 décamètre cube, 10 décamètres cubes donnent 1 hectomètre cube...
• 1 km³ = 1 000 000 000 m³
• 1 hm³ = 1 000 000 m³
• 1 dam³ = 1 000 m³
• 1 dm³ = 0,001 m³
• 1 cm³ = 0,000001 m³
• 1 mm³ = 0,000000001 m³
2. Les unités de contenance
Les unités de contenance mesurent la capacité d'un récipient. L'unité de référence est le litre (L).
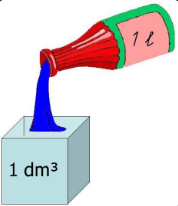
3. Lien entre volume et contenance
1 litre = 1 décimètre cube
1 L = 1 dm³
• \(2,5\) L = \(2,5\) dm³ = \(0,0025\) m³
• \(750\) mL = \(0,75\) L = \(0,75\) dm³
• \(3\) m³ = \(3000\) dm³ = \(3000\) L
177 mL = 0,177 dm³ = 0,177 L
IV. Applications pratiques
1. Calculs de volume dans la vie quotidienne
• Réservoir d'eau : Calculer la capacité d'un réservoir cylindrique
• Emballage : Déterminer le volume d'une boîte pour optimiser le transport
• Construction : Calculer la quantité de béton nécessaire pour une fondation
• Cuisine : Adapter les quantités d'ingrédients selon la taille du récipient
2. Problèmes résolus
Un aquarium a la forme d'un pavé droit de dimensions \(60\) cm × \(30\) cm × \(40\) cm. Quel est son volume en litres ?
\(V = 60 \times 30 \times 40 = 72\,000\) cm³
\(72\,000\) cm³ = \(72\) dm³ = \(72\) L
Une bouteille cylindrique a un rayon de \(4\) cm et une hauteur de \(20\) cm. Quelle est sa capacité en millilitres ?
\(V = \pi \times 4^2 \times 20 = \pi \times 16 \times 20 = 320\pi\) cm³
\(320\pi\) cm³ ≈ \(1005\) cm³ = \(1005\) mL
V. Méthodes de vérification
Vérification par estimation
Estimer le résultat pour vérifier la cohérence.
• Estimation : \(5 \times 5 \times 5 = 125\) cm³
• Calcul exact : \(5^3 = 125\) cm³ ✓
Vérification par unités
Vérifier que les unités du résultat sont cohérentes.
Résumé
• Les polyèdres ont des faces polygonales (prismes, pyramides)
• Les solides de révolution sont obtenus par rotation (cylindre, cône, sphère)
• Le volume mesure l'espace occupé par un solide
• Les formules principales :
- Cube : \(V = c^3\)
- Pavé droit : \(V = L \times l \times h\)
- Cylindre : \(V = \pi \times r^2 \times h\)
- Sphère : \(V = \frac{4}{3} \times \pi \times r^3\)
• 1 L = 1 dm³ (lien volume-contenance)
• Les unités doivent être cohérentes dans les calculs
Exercices d'application
- Calculer le volume d'un cube d'arête \(6\) cm
- Déterminer le volume d'un pavé droit de dimensions \(12\) cm × \(8\) cm × \(5\) cm
- Calculer la capacité en litres d'un cylindre de rayon \(3\) cm et de hauteur \(15\) cm
- Convertir \(2,5\) L en cm³
- Un réservoir sphérique a un rayon de \(2\) m. Quel est son volume en m³ ?
- Une boîte de \(2\) L contient des cubes de \(1\) cm d'arête. Combien de cubes peut-on y mettre ?