Définition :
Deux figures sont symétriques par rapport à une droite lorsqu'elles se superposent par pliage suivant cette droite.

Propriétés importantes :

• Les figures symétriques ont la même forme et la même taille

• Elles sont inversées comme dans un miroir

• Chaque point d'une figure a son correspondant dans l'autre figure

• La droite de symétrie est appelée axe de symétrie

Exemple concret :

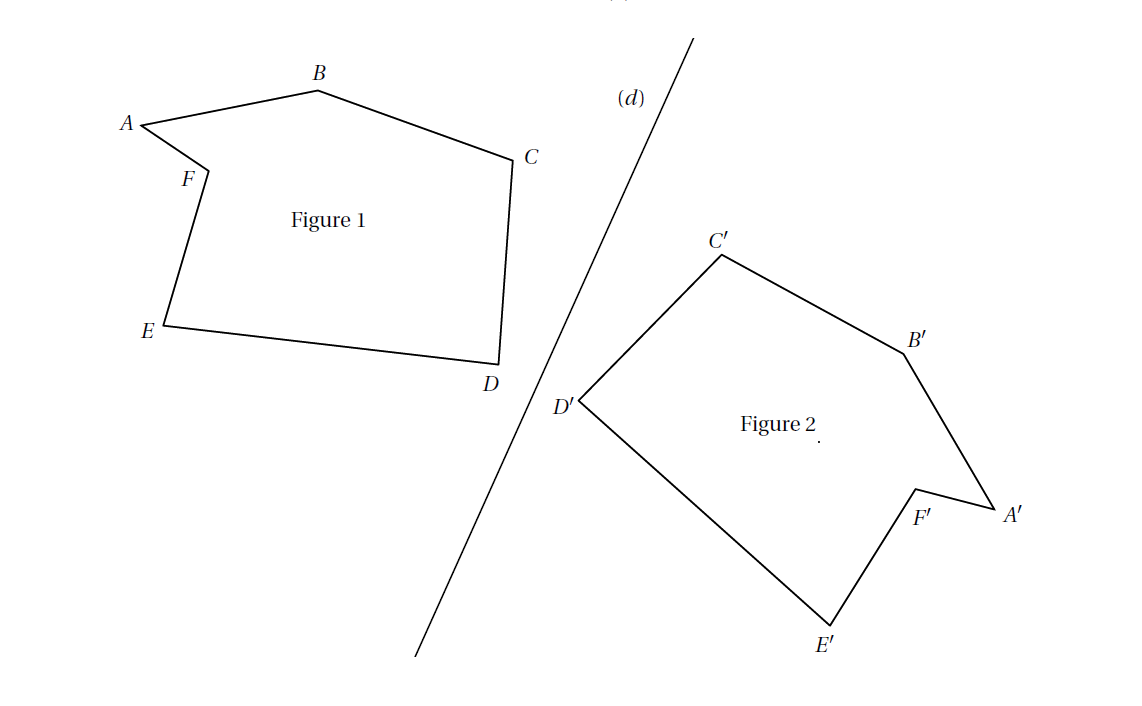
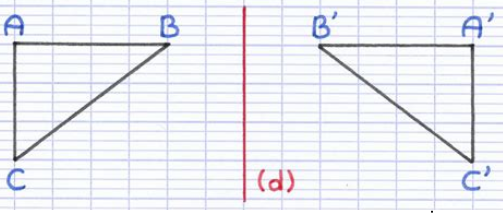
Sur la figure ci-dessus, la Figure 1 est le symétrique de la Figure 2 par rapport à la droite \(d\).

• Les points \(A\) et \(A'\) sont symétriques

• Les points \(B\) et \(B'\) sont symétriques

• Et ainsi de suite pour tous les points...

Définition :
La médiatrice d'un segment est la droite perpendiculaire à ce segment et qui coupe ce segment en son milieu.

Propriétés de la médiatrice :

• Elle est perpendiculaire au segment (angle de \(90°\))

• Elle passe par le milieu du segment

• Tous les points de la médiatrice sont équidistants des extrémités du segment

• Elle est un axe de symétrie du segment

Exemple :

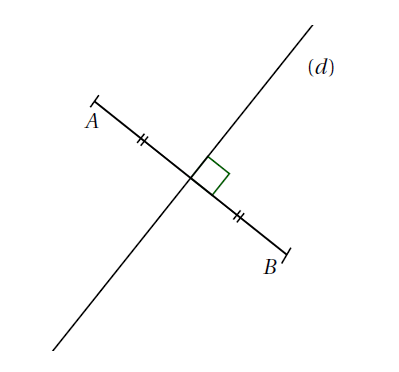
Sur la figure, la droite \(d\) est la médiatrice du segment \([AB]\) :

• \(d\) est perpendiculaire à \((AB)\)

• \(d\) coupe \([AB]\) en son milieu \(I\)

• \(AI = IB\) (les deux moitiés sont égales)

Définition :
Le symétrique d'un point par rapport à une droite est le point tel que cette droite est la médiatrice du segment joignant les deux points.

Cas particuliers :

• Si le point n'appartient pas à la droite : Son symétrique est un point distinct

• Si le point appartient à la droite : Son symétrique est le point lui-même

Exemple :

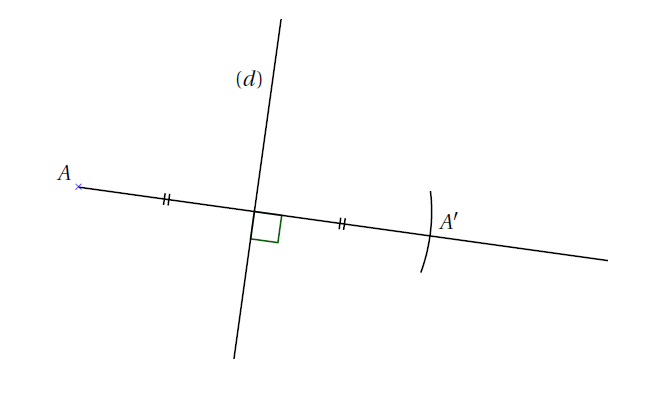
Sur la figure, le point \(A'\) est le symétrique du point \(A\) par rapport à la droite \(d\) :

• La droite \(d\) est la médiatrice du segment \([AA']\)

• \(d\) est perpendiculaire à \([AA']\)

• \(d\) coupe \([AA']\) en son milieu

Méthode de construction :

Étape 1 : Tracer la perpendiculaire à l'axe de symétrie passant par le point
Étape 2 : Mesurer la distance du point à l'axe
Étape 3 : Reporter cette distance de l'autre côté de l'axe
Étape 4 : Placer le point symétrique à cette distance

Méthode au compas :

• Tracer un arc de cercle centré sur l'axe passant par le point

• Tracer un second arc de même rayon de l'autre côté

• Le point d'intersection est le symétrique

Définition :
Lorsque le symétrique d'une figure par rapport à une droite est la figure elle-même, on dit que cette droite est un axe de symétrie de la figure.

Propriétés :

• Une figure peut avoir plusieurs axes de symétrie

• Les axes de symétrie se coupent souvent au centre de la figure

• Chaque axe divise la figure en deux parties identiques

• Le nombre d'axes de symétrie caractérise certaines figures

Exemples :

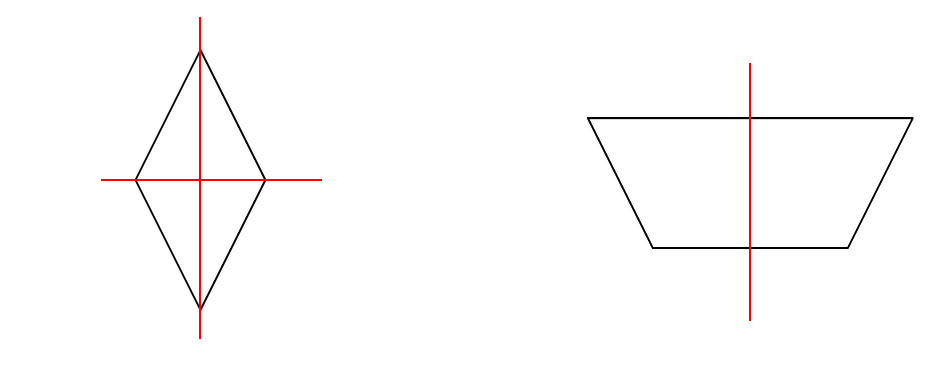
• Figure de gauche : Admet \(2\) axes de symétrie (vertical et horizontal)

• Figure de droite : N'admet qu'\(1\) axe de symétrie (vertical uniquement)

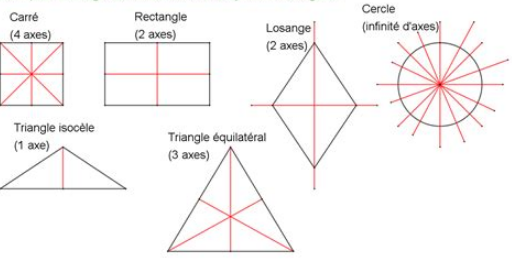
Axes de symétrie des figures géométriques

Principe :
Pour construire le symétrique d'une figure, on construit le symétrique de chacun de ses points par rapport à l'axe de symétrie.

Étapes de construction :

1. Identifier les points caractéristiques de la figure (sommets, points d'intersection)
   
2. Construire le symétrique de chaque point par rapport à l'axe
   
3. Relier les points symétriques dans le même ordre que l'original
   
4. Vérifier la construction en pliant le long de l'axe

Exemple :

Pour construire le symétrique du triangle \(ABC\) par rapport à la droite \(d\) :

• Construire \(A'\) symétrique de \(A\)

• Construire \(B'\) symétrique de \(B\)

• Construire \(C'\) symétrique de \(C\)

• Tracer le triangle \(A'B'C'\)

Exemples de symétrie dans la nature :

• Fleurs : Beaucoup de fleurs ont des axes de symétrie (tulipe, marguerite)

• Papillons : Leurs ailes sont symétriques par rapport à leur corps

• Feuilles : Souvent symétriques par rapport à leur nervure centrale

• Cristaux : Formes géométriques parfaitement symétriques

• Visages : Le visage humain présente une symétrie approximative

Utilisations artistiques :

• Architecture : Façades symétriques des bâtiments classiques

• Design : Logos et motifs décoratifs

• Art islamique : Motifs géométriques complexes

• Orfèvrerie : Bijoux et objets décoratifs

• Photographie : Compositions équilibrées

Objets symétriques :

• Miroirs : Créent des images symétriques

• Écriture : Certaines lettres ont des axes de symétrie

• Emballages : Formes symétriques pour l'esthétique

• Mobilier : Tables, chaises, armoires symétriques

• Véhicules : Voitures, avions, bateaux symétriques

Énoncé :

Construire le symétrique du quadrilatère \(ABCD\) par rapport à la droite \(d\).

Solution :

1. Construire \(A'\) symétrique de \(A\) par rapport à \(d\)
   
2. Construire \(B'\) symétrique de \(B\) par rapport à \(d\)
   
3. Construire \(C'\) symétrique de \(C\) par rapport à \(d\)
   
4. Construire \(D'\) symétrique de \(D\) par rapport à \(d\)
   
5. Tracer le quadrilatère \(A'B'C'D'\)

Énoncé :

Combien d'axes de symétrie possède un hexagone régulier ?

Solution :

Un hexagone régulier possède \(6\) axes de symétrie :

• \(3\) axes passant par les sommets opposés

• \(3\) axes passant par les milieux des côtés opposés

Méthode :

Plier la feuille le long de l'axe de symétrie. Les deux parties doivent se superposer parfaitement.

Avantages :

• Méthode simple et visuelle

• Permet de vérifier rapidement

• Fonctionne pour toutes les figures

Méthode :

Mesurer les distances des points correspondants à l'axe de symétrie. Elles doivent être égales.

Précision :

• Méthode plus précise que le pliage

• Permet de détecter les petites erreurs

• Nécessite un instrument de mesure

Points essentiels à retenir :

• La symétrie axiale transforme une figure en son image miroir

• L'axe de symétrie est la médiatrice du segment joignant deux points symétriques

• Une figure peut avoir plusieurs axes de symétrie ou aucun

• Les figures de base ont un nombre caractéristique d'axes de symétrie

• La construction se fait point par point

• La vérification peut se faire par pliage ou par mesure

• Applications nombreuses dans la nature, l'art et la vie quotidienne

Exercices pratiques :

1. Construire le symétrique du point \(P\) par rapport à la droite \(d\)
   
2. Tracer tous les axes de symétrie d'un carré
   
3. Construire le symétrique du triangle \(ABC\) par rapport à la droite \(d\)
   
4. Combien d'axes de symétrie possède un rectangle ?
   
5. Vérifier par pliage qu'une figure est symétrique
   
6. Construire le symétrique d'une lettre de l'alphabet par rapport à un axe vertical