Fonction Logarithme Neperien
Terminale
COURS: Fonction Logarithme Népérien
Introduction
La fonction logarithme népérien est la fonction réciproque de la fonction exponentielle. Elle joue un rôle fondamental en analyse mathématique et trouve de nombreuses applications en sciences. Ce chapitre explore ses propriétés, son sens de variation et ses propriétés algébriques.
I. Définition de la fonction logarithme népérien
1. Définition par la fonction réciproque
Pour tout réel \(x \in ]0; +\infty[\), il existe un unique réel \(y\) tel que \(e^y = x\).
La fonction logarithme népérien, notée \(\ln\), est la fonction définie sur \(]0; +\infty[\) qui à tout réel \(x > 0\), associe le réel noté \(\ln(x)\) dont l'exponentielle est \(x\).
L'image d'un réel strictement positif \(x\) par la fonction \(\ln\) se note souvent \(\ln x\) au lieu de \(\ln(x)\).
- Pour tout réel \(x > 0\) et tout réel \(y\), \(x = e^y\) équivaut à \(y = \ln x\)
- Pour tout réel \(x > 0\), \(e^{\ln x} = x\)
- Pour tout réel \(x\), \(\ln(e^x) = x\)
2. Preuves et propriétés fondamentales
(1) et (2) se déduisent directement de la définition.
(3) Pour tout réel \(x\), si \(y = \ln(e^x)\) alors d'après (1) \(e^x = e^y\) donc \(x = y\).
\(\ln 1 = 0\). En effet \(e^0 = 1\) et d'après (1) ceci équivaut à \(\ln 1 = 0\).
\(\ln e = 1\). En effet \(e^1 = e\) et d'après (1) ceci équivaut à \(\ln e = 1\).
Pour tout réel \(\lambda\), l'équation \(\ln x = \lambda\) a pour unique solution \(x = e^\lambda\) d'après (1).
Dans un repère orthonormal, les courbes représentatives des fonctions exponentielles et logarithme népérien sont symétriques par rapport à la droite d'équation \(y = x\).
On note \(\mathcal{C}\) et \(\mathcal{C}'\) les courbes représentatives des fonctions \(\exp\) et \(\ln\).
Dire que \(M'(x; y)\) appartient à \(\mathcal{C}'\) équivaut à dire que \(M(y; x)\) appartient à \(\mathcal{C}\).
\(\mathcal{C}\) et \(\mathcal{C}'\) sont donc symétriques par rapport à la droite \(y = x\).
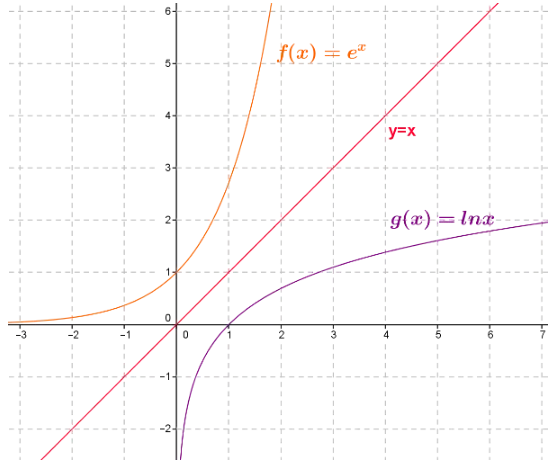
II. Sens de variation de la fonction logarithme népérien sur ]0; +∞[
La fonction logarithme népérien est strictement croissante sur \(]0; +\infty[\).
\(a\) et \(b\) sont deux réels tels que \(0 < a < b\), c'est à dire que \(e^{\ln a} < e^{\ln b}\).
La fonction exponentielle est strictement croissante sur \(\mathbb{R}\) donc \(\ln a < \ln b\).
Pour tous réels \(a\) et \(b\) de \(]0; +\infty[\) :
• \(\ln a = \ln b\) équivaut à \(a = b\) et \(\ln a < \ln b\) équivaut à \(a < b\)
• \(\ln a > 0\) équivaut à \(a > 1\) et \(\ln a < 0\) équivaut à \(0 < a < 1\)
III. Les propriétés algébriques
1. Relation fonctionnelle
Pour tous réels \(a\) et \(b\) de \(]0; +\infty[\) : \(\ln(ab) = \ln a + \ln b\)
\(a\) et \(b\) sont deux réels strictement positifs. On note \(A = \ln(ab)\) et \(B = \ln a + \ln b\) alors
\(e^A = ab\) et \(e^B = e^{\ln a + \ln b} = e^{\ln a} \times e^{\ln b} = ab\)
donc \(e^A = e^B\) d'où \(A = B\) puisque la fonction exponentielle est bijective sur \(\mathbb{R}\).
2. Logarithme d'un quotient
Pour tout réel \(a \in ]0; +\infty[\) : \(\ln\left(\frac{1}{a}\right) = -\ln a\)
Pour \(a > 0\), on écrit \(a \times \frac{1}{a} = 1\) donc \(\ln\left(a \times \frac{1}{a}\right) = \ln 1\)
c'est à dire \(\ln(a) + \ln\left(\frac{1}{a}\right) = 0\) d'où \(\ln\left(\frac{1}{a}\right) = -\ln(a)\).
Pour tous réels \(a\) et \(b\) de \(]0; +\infty[\) : \(\ln\left(\frac{a}{b}\right) = \ln(a) - \ln(b)\)
Pour \(a > 0\) et \(b > 0\), \(\ln\left(\frac{a}{b}\right) = \ln\left(a \times \frac{1}{b}\right) = \ln a + \ln\left(\frac{1}{b}\right) = \ln a - \ln(b)\).
3. Logarithme d'un produit de nombres réels strictement positifs
Pour tous réels \(a_1, a_2, a_3, \ldots, a_n \in ]0; +\infty[\) : \(\ln(a_1 a_2 a_3 \cdots a_n) = \ln a_1 + \ln a_2 + \ln a_3 + \cdots + \ln a_n\)
Cette formule généralise la relation fonctionnelle établie dans le paragraphe 1. et peut se démontrer par récurrence.
Pour tout réel a de ]0; +∞[ et tout entier relatif n, ln(aⁿ) = n ln a.
La démonstration de cette propriété se fait par récurrence et sur le signe de n.
4. Logarithme d'une racine carrée
Pour tout réel a de ]0; +∞[, ln(√a) = ½ ln a.
Pour a > 0, (√a)² = a donc ln((√a)²) = ln a
ainsi 2ln(√a) = ln a
d'où ln(√a) = ½ ln a
IV. Limites de la fonction logarithme népérien
1. Limites aux bornes du domaine
• lim(x→0⁺) ln x = -∞
• lim(x→+∞) ln x = +∞
Ces limites se déduisent des limites de la fonction exponentielle par symétrie par rapport à la droite y = x.
2. Croissances comparées
Soit n un entier naturel non nul.
• lim(x→+∞) (ln x)/xⁿ = 0
• lim(x→0⁺) x ln x = 0
La première limite traduit le fait que toute puissance de x croît plus vite que ln x. La seconde limite est importante pour l'étude de fonctions.
V. Dérivée de la fonction logarithme népérien
La fonction logarithme népérien est dérivable sur ]0; +∞[ et pour tout x > 0 :
(ln x)' = 1/x
Si u est une fonction dérivable et strictement positive sur un intervalle I, alors :
(ln(u(x)))' = u'(x)/u(x)
• Si f(x) = ln(2x + 1) avec x > -1/2, alors f'(x) = 2/(2x + 1)
• Si g(x) = ln(x²) avec x ≠ 0, alors g'(x) = 2x/x² = 2/x
• Si h(x) = ln(cos x) avec cos x > 0, alors h'(x) = -sin x/cos x = -tan x
VI. Équations et inéquations avec des logarithmes
1. Équations simples
Résoudre ln x = 3
Résoudre ln(2x - 1) = ln(x + 3)
Équation : 2x - 1 = x + 3
Solution : x = 4
2. Inéquations
Résoudre ln x ≥ 2
Équivalence : x ≥ e²
Solution : S = [e²; +∞[
Résoudre ln(x - 1) < ln(2x + 1)
Inéquation : x - 1 < 2x + 1 ⟺ -2 < x
Solution : S = ]1; +∞[
VII. Applications et études de fonctions
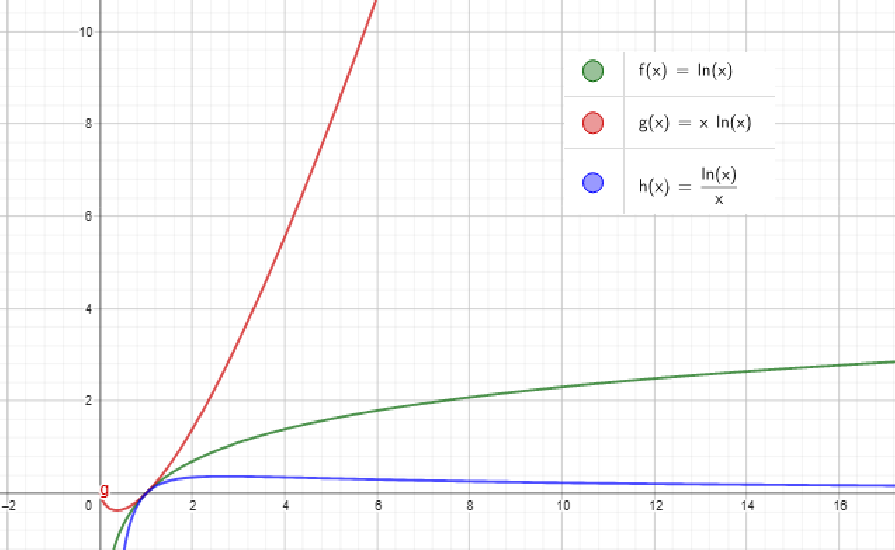
1. Fonction x ↦ x ln x
Dérivée : f'(x) = ln x + x × (1/x) = ln x + 1
Signe de f' : f'(x) > 0 ⟺ ln x > -1 ⟺ x > e⁻¹ = 1/e
Variations :
• f décroissante sur ]0; 1/e[
• f croissante sur ]1/e; +∞[
• Minimum en x = 1/e : f(1/e) = -1/e
• lim(x→0⁺) x ln x = 0
• lim(x→+∞) x ln x = +∞
2. Fonction x ↦ ln x/x
Dérivée : g'(x) = (1/x × x - ln x × 1)/x² = (1 - ln x)/x²
Signe de g' : g'(x) > 0 ⟺ 1 - ln x > 0 ⟺ ln x < 1 ⟺ x < e
Variations :
• g croissante sur ]0; e[
• g décroissante sur ]e; +∞[
• Maximum en x = e : g(e) = 1/e
• lim(x→0⁺) (ln x)/x = -∞
• lim(x→+∞) (ln x)/x = 0
VIII. Primitive et intégration
Une primitive de la fonction x ↦ 1/x sur ]0; +∞[ est la fonction x ↦ ln x.
Plus généralement, si u est une fonction dérivable et strictement positive sur un intervalle I, alors une primitive de u'/u est ln u.
• ∫ 1/x dx = ln x + C (sur ]0; +∞[)
• ∫ 2x/(x² + 1) dx = ln(x² + 1) + C
• ∫ tan x dx = ∫ sin x/cos x dx = -ln|cos x| + C
• ∫ 1/(2x + 3) dx = ½ ln|2x + 3| + C
IX. Équations différentielles
1. Équation y' = ay (a constante)
Les solutions de l'équation différentielle y' = ay (où a est une constante réelle) sont les fonctions de la forme :
\(y(x) = Ce^{ax}\)
où C est une constante réelle.
2. Résolution par séparation des variables
Pour résoudre y' = ay avec y(x₀) = y₀ :
- Séparer les variables : dy/y = a dx
- Intégrer : ∫ dy/y = ∫ a dx
- Obtenir : ln|y| = ax + C
- Donc : \(y = Ke^{ax}\) où \(K = \pm e^C\)
- Utiliser la condition initiale pour déterminer K
Résumé
• Définition : ln est la fonction réciproque de exp, définie sur ]0; +∞[
• Propriétés fondamentales : \(\ln(e^x) = x\) et \(e^{\ln x} = x\)
• Valeurs particulières : \(\ln(1) = 0\) et \(\ln(e) = 1\)
• Sens de variation : ln est strictement croissante sur \(]0; +\infty[\)
• Propriétés algébriques : \(\ln(ab) = \ln a + \ln b\), \(\ln(a/b) = \ln a - \ln b\), \(\ln(a^n) = n \ln a\)
• Limites : \(\lim_{x \to 0^+} \ln x = -\infty\), \(\lim_{x \to +\infty} \ln x = +\infty\)
• Dérivée : \((\ln x)' = \frac{1}{x}\), \((\ln u)' = \frac{u'}{u}\)
• Primitive : \(\int \frac{1}{x} dx = \ln|x| + C\)
• Croissances comparées : ln x croît moins vite que toute puissance positive de x
Exercices d'application
- Calculer \(\ln(8) - \ln(2) + \ln(1/4)\)
- Résoudre l'équation \(\ln(x - 1) + \ln(x + 1) = \ln(8)\)
- Étudier les variations de \(f(x) = \ln(x^2)\)
- Déterminer les limites de \(g(x) = x \ln x\) en \(0^+\) et \(+\infty\)
- Calculer la dérivée de \(h(x) = \ln(\sqrt{x^2 + 1})\)
- Résoudre l'équation différentielle \(y' - 2y = 0\) avec \(y(0) = 3\)
- Calculer \(\int_1^e \frac{1 + \ln x}{x} dx\)