Fonctions Continues
Terminale
CONTINUITÉ DES FONCTIONS
I. NOTION DE CONTINUITÉ
1) Définition intuitive
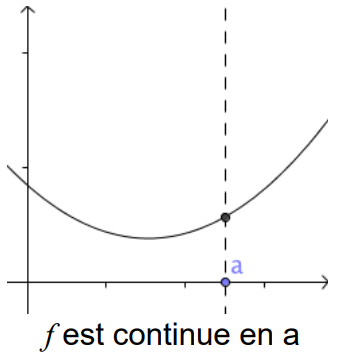
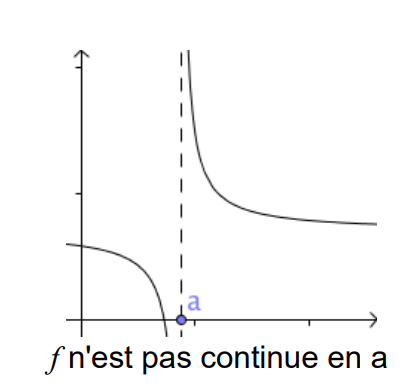
Une fonction \(f\) est continue en un point \(a\) si on peut tracer sa courbe représentative en ce point "sans lever le crayon".
La continuité d'une fonction en un point signifie qu'il n'y a pas de "saut" ou de "trou" dans la courbe en ce point.
2) Définition mathématique
Soit \(f\) une fonction définie sur un intervalle \(I\) contenant un réel \(a\).
• \(f\) est continue en \(a\) si \(\lim_{x \to a} f(x) = f(a)\)
• \(f\) est continue sur \(I\) si \(f\) est continue en tout point de \(I\)
• Les fonctions \(x \mapsto |x|\), \(x \mapsto x^n\) (\(n \in \mathbb{N}\)) et plus généralement les fonctions polynômes sont continues sur \(\mathbb{R}\)
• Les fonctions \(f(x) = \sin x\) et \(g(x) = \cos x\) sont continues sur \(\mathbb{R}\)
• La fonction \(h(x) = \sqrt{x}\) est continue sur \([0; +\infty[\)
• La fonction \(k(x) = \frac{1}{x}\) est continue sur \(]-\infty; 0[\) et sur \(]0; +\infty[\)
II. THÉORÈME FONDAMENTAL
Une fonction dérivable sur un intervalle \(I\) est continue sur cet intervalle.
La réciproque est fausse ! Une fonction peut être continue sans être dérivable (exemple : \(f(x) = |x|\) en 0).
III. ÉTUDE DE LA CONTINUITÉ D'UNE FONCTION
Méthode d'étude
Pour étudier la continuité d'une fonction \(f\) :
- Identifier les points "suspects" (changement de définition, valeurs interdites)
- Calculer les limites à gauche et à droite en ces points
- Comparer avec la valeur de la fonction en ces points
- Conclure sur la continuité
Exemple d'application
On considère la fonction \(f\) définie sur \(\mathbb{R}\) par :
\[f(x) = \begin{cases}
-x + 2 & \text{si } x < 3 \\
x - 4 & \text{si } 3 \leq x < 5 \\
-2x + 13 & \text{si } x \geq 5
\end{cases}\]
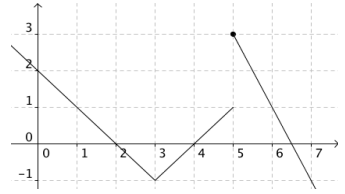
• En \(x = 3\) :
- \(\lim_{x \to 3^-} f(x) = \lim_{x \to 3^-} (-x + 2) = -1\)
- \(\lim_{x \to 3^+} f(x) = \lim_{x \to 3^+} (x - 4) = -1\)
- \(f(3) = 3 - 4 = -1\)
Donc \(f\) est continue en 3.
• En \(x = 5\) :
- \(\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} (x - 4) = 1\)
- \(\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} (-2x + 13) = 3\)
Les limites à gauche et à droite sont différentes, donc \(f\) n'est pas continue en 5.
IV. THÉORÈME DES VALEURS INTERMÉDIAIRES
1) Énoncé du théorème
Soit \(f\) une fonction définie et continue sur un intervalle \([a; b]\).
Pour tout réel \(k\) compris entre \(f(a)\) et \(f(b)\), il existe au moins un réel \(c\) entre \(a\) et \(b\) tel que \(f(c) = k\).
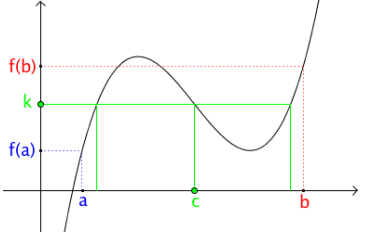
2) Conséquences
Sous ces conditions, l'équation \(f(x) = k\) admet au moins une solution dans l'intervalle \([a; b]\).
Ce théorème est très utile pour :
• Résoudre des équations
• Montrer l'existence de solutions
• Encadrer des solutions
3) Cas particulier : fonction strictement monotone
Si \(f\) est continue et strictement monotone sur \([a; b]\), alors pour tout \(k\) compris entre \(f(a)\) et \(f(b)\), l'équation \(f(x) = k\) admet une unique solution dans \([a; b]\).
V. EXEMPLES D'APPLICATION
Exemple 1 : Résolution d'équation
Montrer que l'équation \(x^3 - 3x + 1 = 0\) admet au moins une solution dans \([0; 2]\).
Soit \(f(x) = x^3 - 3x + 1\).
• \(f\) est continue sur \(\mathbb{R}\) (fonction polynôme)
• \(f(0) = 1\) et \(f(2) = 8 - 6 + 1 = 3\)
• \(0\) est compris entre \(f(0) = 1\) et \(f(2) = 3\)
D'après le théorème des valeurs intermédiaires, l'équation \(f(x) = 0\) admet au moins une solution dans \([0; 2]\).
Exemple 2 : Encadrement de solution
Encadrer la solution de l'équation \(e^x = x + 2\) à \(10^{-2}\) près.
Soit \(f(x) = e^x - x - 2\).
• \(f\) est continue sur \(\mathbb{R}\)
• \(f(0) = 1 - 0 - 2 = -1 < 0\)
• \(f(1) = e - 1 - 2 \approx 2,72 - 3 = -0,28 < 0\)
• \(f(2) = e^2 - 2 - 2 \approx 7,39 - 4 = 3,39 > 0\)
La solution est dans \([1; 2]\).
En affinant : \(f(1,5) \approx 0,48 > 0\), donc la solution est dans \([1; 1,5]\).
\(f(1,2) \approx -0,07 < 0\), donc la solution est dans \([1,2; 1,5]\).
\(f(1,3) \approx 0,17 > 0\), donc la solution est dans \([1,2; 1,3]\).
La solution est encadrée par \(1,2 < \alpha < 1,3\).
VI. RÉSUMÉ
• Une fonction est continue en un point si sa limite en ce point est égale à sa valeur
• Toute fonction dérivable est continue
• Le théorème des valeurs intermédiaires permet de résoudre des équations
• La continuité est essentielle pour l'étude des fonctions
• Pour étudier la continuité : calculer les limites à gauche et à droite
• Pour résoudre \(f(x) = k\) : utiliser le TVI sur un intervalle approprié
• Pour encadrer une solution : affiner l'intervalle par dichotomie