Fonctions Trigonométriques
Terminale
FONCTIONS TRIGONOMÉTRIQUES
I. DÉFINITION DES FONCTIONS SINUS ET COSINUS
1) Le cercle trigonométrique
Le plan est muni d'un repère orthonormé \((O; \vec{i}, \vec{j})\).
À tout réel \(t\), on associe un unique point \(M\) du cercle trigonométrique (cercle de centre \(O\) et de rayon 1) tel que \(t\) soit la mesure de l'angle orienté \((\vec{i}, \overrightarrow{OM})\) en radians.
Le point \(M\) a pour coordonnées \((\cos t; \sin t)\).
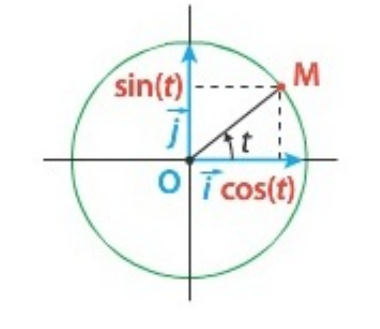
Pour tout réel \(t \in \mathbb{R}\), les valeurs de \(\cos t\) et \(\sin t\) sont toujours comprises entre -1 et 1. Autrement dit :
\( -1 \le \cos t \le 1 \)
\( -1 \le \sin t \le 1 \)
2) Définition des fonctions sinus et cosinus
- La fonction qui à tout réel \(x\) fait correspondre l'abscisse \(\cos x\) du point \(M\) est appelée la fonction cosinus et est notée \(\cos\).
- La fonction qui à tout réel \(x\) fait correspondre l'ordonnée \(\sin x\) du point \(M\) est appelée la fonction sinus et est notée \(\sin\).
II. PROPRIÉTÉS DES FONCTIONS SINUS ET COSINUS
1) Parité des fonctions sinus et cosinus
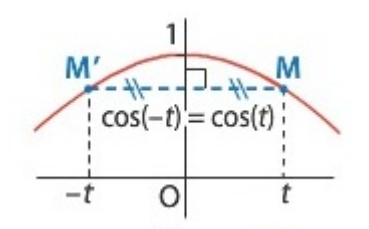
- Pour tout réel \(x\), \(\cos(-x) = \cos x\) : on dit que la fonction cosinus est paire sur \(\mathbb{R}\).
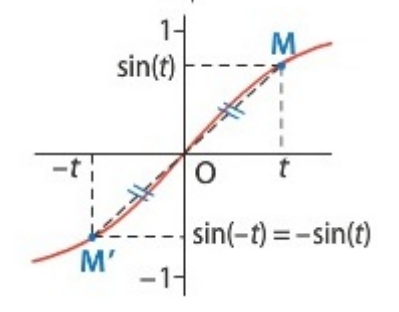
- Pour tout réel \(x\), \(\sin(-x) = -\sin x\) : on dit que la fonction sinus est impaire sur \(\mathbb{R}\).
2) Interprétation graphique de la parité
Le plan est muni d'un repère orthonormal \((O; \vec{i}, \vec{j})\).
* Pour la fonction cosinus (paire) :
Les points \(M(x; \cos x)\) et \(M'(-x; \cos(-x))\) sont symétriques par rapport à l'axe des ordonnées \((O; \vec{j})\). La courbe représentative de la fonction cosinus est donc symétrique par rapport à l'axe des ordonnées.
* Pour la fonction sinus (impaire) :
Les points \(M(x; \sin x)\) et \(M'(-x; \sin(-x))\) sont symétriques par rapport à l'origine \(O\) du repère. La courbe représentative de la fonction sinus est donc symétrique par rapport à l'origine \(O\) du repère.
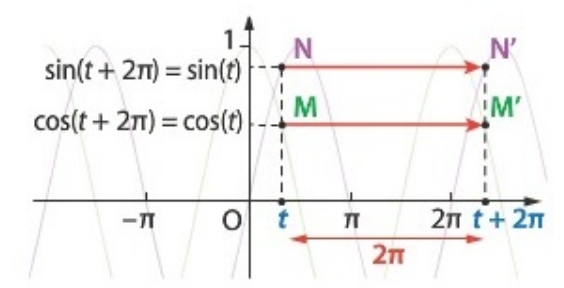
3) Périodicité des fonctions sinus et cosinus
Pour tout réel \(x\), on a :
\( \cos(x + 2\pi) = \cos x \)
\( \sin(x + 2\pi) = \sin x \)
On dit que les fonctions cosinus et sinus sont périodiques de période \(2\pi\) (ou « \(2\pi\)-périodiques »). Cela signifie que leurs courbes représentatives se répètent tous les \(2\pi\) sur l'axe des abscisses.
III. DÉRIVÉES DES FONCTIONS TRIGONOMÉTRIQUES
1) Dérivées des fonctions sinus et cosinus
Les fonctions sinus et cosinus sont définies et dérivables sur \(\mathbb{R}\) et :
• Pour tout \(x \in \mathbb{R}\), \(\sin' x = \cos x\)
• Pour tout \(x \in \mathbb{R}\), \(\cos' x = -\sin x\)
2) Dérivées de fonctions composées
Soit \(u\) une fonction définie et dérivable sur un intervalle \(I\). Alors les fonctions \(\cos u\) et \(\sin u\) sont dérivables sur \(I\) et :
• \((\cos u)' = -u' \sin u\)
• \((\sin u)' = u' \cos u\)
Soient \(f\) et \(g\) les fonctions définies sur \(\mathbb{R}\) par :
• \(f(x) = \sin(x^2+1)\)
• \(g(x) = \frac{\cos(1+e^x)}{e^x}\)
Déterminer pour tout réel \(x\), \(f'(x)\) et \(g'(x)\).
• Pour \(f(x) = \sin(x^2+1)\) :
On pose \(u(x) = x^2 + 1\), donc \(u'(x) = 2x\)
\(f'(x) = u'(x) \cos u(x) = 2x \cos(x^2+1)\)
• Pour \(g(x) = \frac{\cos(1+e^x)}{e^x}\) :
On pose \(u(x) = 1+e^x\), donc \(u'(x) = e^x\)
\(g'(x) = \frac{-u'(x) \sin u(x) \cdot e^x - \cos u(x) \cdot e^x}{(e^x)^2}\)
\(g'(x) = \frac{-e^x \sin(1+e^x) - \cos(1+e^x)}{e^x}\)
\(g'(x) = -\sin(1+e^x) - \frac{\cos(1+e^x)}{e^x}\)
IV. ÉTUDE DES FONCTIONS SINUS ET COSINUS
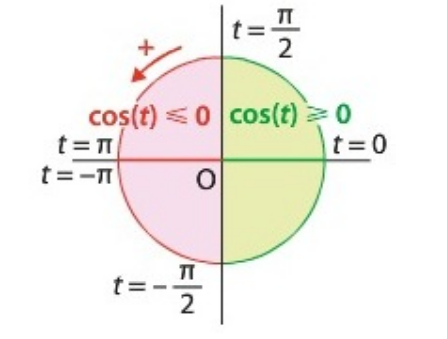
1) Sens de variation de la fonction cosinus
Pour étudier le sens de variation de la fonction cosinus, nous étudions le signe de sa dérivée \(-\sin(x)\).
| \(x\) | \(0\) | \(\pi\) | |
| \(\cos'(x) = -\sin(x)\) | \(0\) | \(-\) | \(0\) |
| \(\cos(x)\) | \(1\) | \(\searrow\) | \(-1\) |
On en déduit le sens de variations de la fonction cosinus sur \([-\pi; \pi]\) par symétrie axiale par rapport à l'axe des ordonnées (car la fonction est paire) :
| \(x\) | \(-\pi\) | \(0\) | \(\pi\) | ||
| \(\cos(x)\) | \(-1\) | \(\nearrow\) | \(1\) | \(\searrow\) | \(-1\) |
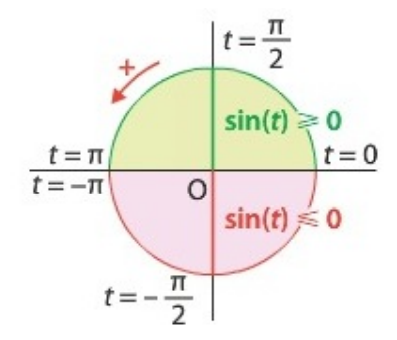
2) Sens de variation de la fonction sinus
Pour étudier le sens de variation de la fonction sinus, nous étudions le signe de sa dérivée \(\cos(x)\).
| \(x\) | \(-\pi\) | \(-\frac{\pi}{2}\) | \(0\) | \(\frac{\pi}{2}\) | \(\pi\) | ||
| \(\sin'(x) = \cos(x)\) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) | ||
| \(\sin(x)\) | \(0\) | \(\searrow\) | \(-1\) | \(\nearrow\) | \(1\) | \(\searrow\) | \(0\) |
3) Courbes représentatives
Voici un tableau des valeurs remarquables pour les fonctions sinus et cosinus :
| \(x\) | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\pi\) |
| \(\sin(x)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) |
| \(\cos(x)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) |
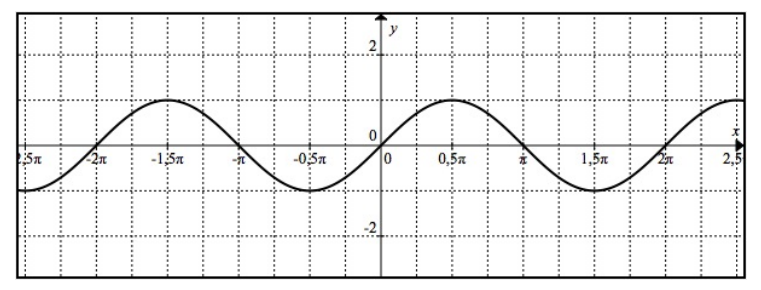
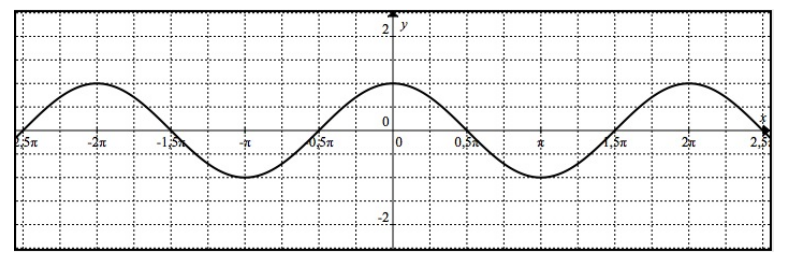
V. LIMITES DES FONCTIONS TRIGONOMÉTRIQUES
Les fonctions sinus et cosinus n'admettent pas de limites en \(+\infty\) ou en \(-\infty\).
En revanche, une fonction « contenant » un sinus ou un cosinus peut admettre une limite en \(+\infty\) ou en \(-\infty\).
• \(\lim_{x \to +\infty} (x^2 + \cos(x)) = +\infty\)
• \(\lim_{x \to +\infty} \frac{\sin(x)}{x} = 0\)
VI. RÉSOLUTION D'ÉQUATIONS ET D'INÉQUATIONS
1) Équations trigonométriques
Soient \(a\) et \(x\) deux nombres réels.
• \(\cos(x) = \cos(a) \Leftrightarrow x = a + 2k\pi\) ou \(x = -a + 2k\pi\), avec \(k \in \mathbb{Z}\)
• \(\sin(x) = \sin(a) \Leftrightarrow x = a + 2k\pi\) ou \(x = \pi - a + 2k\pi\), avec \(k \in \mathbb{Z}\)
• Résoudre dans \(\mathbb{R}\) l'équation : \(\cos(x) = -\frac{1}{2}\)
• Résoudre dans \(]-\pi; \pi]\), puis dans \([0; 3\pi]\), l'équation : \(\sqrt{2}\sin(x) + 3 = 2\)
Premier exemple :
\(\cos(x) = -\frac{1}{2}\)
On sait que \(\cos\left(\frac{2\pi}{3}\right) = -\frac{1}{2}\)
Donc \(\cos(x) = \cos\left(\frac{2\pi}{3}\right)\)
D'où \(x = \frac{2\pi}{3} + 2k\pi\) ou \(x = -\frac{2\pi}{3} + 2k\pi\), avec \(k \in \mathbb{Z}\)
\(\sqrt{2}\sin(x) + 3 = 2\)
\(\sqrt{2}\sin(x) = -1\)
\(\sin(x) = -\frac{1}{\sqrt{2}} = -\frac{\sqrt{2}}{2}\)
On sait que \(\sin\left(-\frac{\pi}{4}\right) = -\frac{\sqrt{2}}{2}\)
Donc \(\sin(x) = \sin\left(-\frac{\pi}{4}\right)\)
D'où \(x = -\frac{\pi}{4} + 2k\pi\) ou \(x = \pi - \left(-\frac{\pi}{4}\right) + 2k\pi = \frac{5\pi}{4} + 2k\pi\), avec \(k \in \mathbb{Z}\)
Dans \(]-\pi; \pi]\) : \(x = -\frac{\pi}{4}\)
Dans \([0; 3\pi]\) : \(x = \frac{5\pi}{4}\) et \(x = \frac{5\pi}{4} + 2\pi = \frac{13\pi}{4}\)
2) Inéquations trigonométriques
Résoudre dans \(]-\pi; \pi]\) puis dans \([0; 2\pi]\) l'inéquation : \(\cos(x) \leq \frac{\sqrt{3}}{2}\)
On sait que \(\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\)
L'inéquation \(\cos(x) \leq \frac{\sqrt{3}}{2}\) devient \(\cos(x) \leq \cos\left(\frac{\pi}{6}\right)\)
En utilisant les variations de la fonction cosinus sur \([-\pi; \pi]\) :
• Sur \(\left[-\pi; -\frac{\pi}{6}\right]\) : \(\cos(x) \leq \frac{\sqrt{3}}{2}\)
• Sur \(\left[\frac{\pi}{6}; \pi\right]\) : \(\cos(x) \leq \frac{\sqrt{3}}{2}\)
Donc dans \(]-\pi; \pi]\) : \(x \in \left]-\pi; -\frac{\pi}{6}\right] \cup \left[\frac{\pi}{6}; \pi\right]\)
Dans \([0; 2\pi]\) : \(x \in \left[\frac{\pi}{6}; \frac{11\pi}{6}\right]\)
VII. RÉSUMÉ
• Les fonctions sinus et cosinus sont définies sur \(\mathbb{R}\) et périodiques de période \(2\pi\)
• La fonction cosinus est paire, la fonction sinus est impaire
• Leurs dérivées sont : \(\sin' x = \cos x\) et \(\cos' x = -\sin x\)
• Elles n'admettent pas de limites en \(\pm\infty\)
• Les équations trigonométriques se résolvent en utilisant les propriétés de périodicité
• Pour étudier les variations : utiliser les dérivées
• Pour résoudre \(\cos(x) = \cos(a)\) : \(x = a + 2k\pi\) ou \(x = -a + 2k\pi\)
• Pour résoudre \(\sin(x) = \sin(a)\) : \(x = a + 2k\pi\) ou \(x = \pi - a + 2k\pi\)
• Pour les inéquations : utiliser les variations et la périodicité