Integration
Terminale
COURS: Le Calcul Intégral
Introduction
Le calcul intégral est une branche fondamentale des mathématiques qui permet de calculer des aires, des volumes et de résoudre de nombreux problèmes pratiques. Ce chapitre explore la notion d'intégrale, ses propriétés et ses applications géométriques.
I. Notion d'intégrale
1. Aire sous la courbe
On considère une fonction \(f\) continue et positive sur un intervalle \([a; b]\). On appelle aire sous la courbe de \(f\) sur \([a; b]\) l'aire du domaine plan délimité par :
• L'axe des abscisses
• Les droites d'équations \(x = a\) et \(x = b\)
• La courbe représentative de la fonction \(f\)
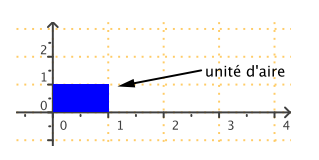
L'unité d'aire (u.a.) est l'aire du rectangle défini par les vecteurs unitaires \(\vec{i}\) et \(\vec{j}\) du repère orthonormé.
2. Intégrale d'une fonction positive
Soit \(f\) une fonction continue et positive sur \([a; b]\). L'intégrale de \(f\) sur \([a; b]\), notée \(\int_a^b f(t) \, dt\), est l'aire (en unités d'aire) du domaine délimité par l'axe des abscisses, les droites \(x = a\) et \(x = b\), et la courbe représentative de \(f\).
La variable \(t\) est une variable muette : \(\int_a^b f(t) \, dt = \int_a^b f(u) \, du\)
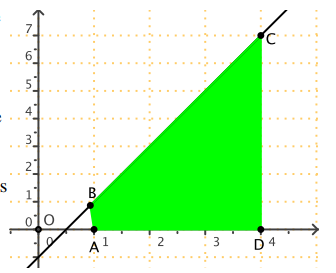
Calculons \(\int_1^4 (2t - 1) \, dt\) où \(f(t) = 2t - 1\) sur \([1; 4]\).
Cette intégrale représente l'aire d'un trapèze de sommets :
• \(A(1; 0)\), \(B(1; 1)\), \(C(4; 7)\), \(D(4; 0)\)
Aire du trapèze = \(\frac{(\text{petite base} + \text{grande base}) \times \text{hauteur}}{2}\)
= \(\frac{(1 + 7) \times 3}{2} = 12\) u.a.
3. Extension à une fonction de signe quelconque
Soit \(f\) une fonction continue sur \([a; b]\) :
• Si \(f \leq 0\) sur \([a; b]\), alors \(\int_a^b f(t) \, dt = -A\) où \(A\) est l'aire
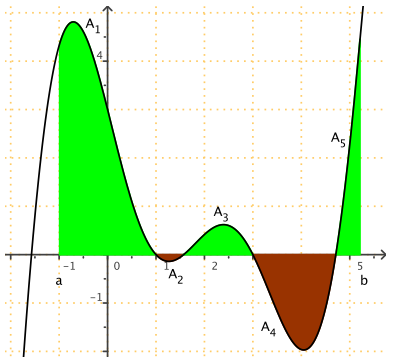
• Si \(f\) est de signe quelconque, on détermine les intervalles où \(f\) est positive et négative, puis :
\(\int_a^b f(t) \, dt = A_1 - A_2 + A_3 - A_4 + A_5\)
4. Valeur moyenne d'une fonction
La valeur moyenne de la fonction \(f\) continue sur \([a; b]\) est le réel :
\(\mu = \frac{1}{b-a} \int_a^b f(t) \, dt\)
II. Propriétés de l'intégrale
1. Propriétés algébriques
Soit \(f\) et \(g\) des fonctions continues sur un intervalle \(I\), et \(a, b, c \in I\) :
• \(\int_a^a f(t) \, dt = 0\)
• \(\int_a^b f(t) \, dt = -\int_b^a f(t) \, dt\)
• Relation de Chasles : \(\int_a^b f(t) \, dt + \int_b^c f(t) \, dt = \int_a^c f(t) \, dt\)
• Linéarité :
- \(\int_a^b k \cdot f(t) \, dt = k \int_a^b f(t) \, dt\) (où \(k \in \mathbb{R}\))
- \(\int_a^b [f(t) + g(t)] \, dt = \int_a^b f(t) \, dt + \int_a^b g(t) \, dt\)
2. Intégrales et inégalités
Soit \(f\) et \(g\) des fonctions continues sur \([a; b]\) avec \(a < b\) :
• Positivité : Si \(f \geq 0\) sur \([a; b]\), alors \(\int_a^b f(t) \, dt \geq 0\)
• Ordre : Si \(f \geq g\) sur \([a; b]\), alors \(\int_a^b f(t) \, dt \geq \int_a^b g(t) \, dt\)
• Inégalité de la moyenne :
Si \(\forall x \in [a; b]\), \(m \leq f(x) \leq M\), alors :
\(m(b-a) \leq \int_a^b f(t) \, dt \leq M(b-a)\)
c'est-à-dire que la valeur moyenne \(\mu\) de \(f\) vérifie \(m \leq \mu \leq M\)
Si \(\forall x \in [a; b]\), \(|f(x)| \leq M\), alors :
\(|\int_a^b f(t) \, dt| \leq M(b-a)\)
III. Primitives d'une fonction
1. Notion de primitive
On considère une fonction \(f\) définie sur un intervalle \(I\). On appelle primitive de \(f\) sur \(I\) toute fonction \(F\) dérivable sur \(I\) telle que pour tout \(x \in I\), \(F'(x) = f(x)\).
• Une primitive de \(f(x) = 2x - 1\) sur \(\mathbb{R}\) est \(F(x) = x^2 - x + 1\)
• Une primitive de \(f(x) = x^2\) sur \(\mathbb{R}\) est \(F(x) = \frac{x^3}{3}\)
2. Ensemble des primitives et conditions initiales
Toute fonction \(f\) continue sur \(I\) admet une infinité de primitives sur \(I\).
Si \(F\) est une primitive de \(f\), alors les autres primitives de \(f\) sont les fonctions de la forme \(F(x) + k\) avec \(k \in \mathbb{R}\).
Soit \(f\) une fonction continue sur un intervalle \(I\), \(x_0 \in I\) et \(y_0 \in \mathbb{R}\).
Alors \(f\) admet une unique primitive \(F\) telle que \(F(x_0) = y_0\) (appelée condition initiale).
La primitive de \(f(x) = x^2\) sur \(\mathbb{R}\) telle que \(F(1) = 2\) est :
\(F(x) = \frac{x^3 + 5}{3}\)
3. Intégrale et primitive
Soit \(f\) une fonction continue sur un intervalle \(I\) et \(a \in I\).
La fonction \(F\) définie par \(F(x) = \int_a^x f(t) \, dt\) est la primitive de \(f\) qui s'annule en \(a\).
La démonstration est faite dans le cas où \(f\) est positive et croissante.
Soit \(x_0 \in I\) et \(x > x_0\). Pour tout \(t \in [x_0; x]\), on a \(f(x_0) \leq f(t) \leq f(x)\) par croissance de \(f\).
Ainsi, par le théorème de la moyenne :
\(f(x_0)(x-x_0) \leq \int_{x_0}^x f(t) \, dt \leq f(x)(x-x_0)\)
En divisant par \((x-x_0)\) et en passant à la limite, on obtient \(F'(x_0) = f(x_0)\).
IV. Théorème fondamental du calcul intégral
1. Le théorème
Soit \(f\) une fonction continue sur un intervalle \(I\) et \(a, b \in I\).
Alors \(\int_a^b f(t) \, dt = F(b) - F(a)\) où \(F\) est une primitive quelconque de \(f\).
2. Notation
\(\int_a^b f(t) \, dt = [F(t)]_a^b = F(b) - F(a)\)
3. Démonstration
Soit \(F\) la primitive de \(f\) qui s'annule en \(a\), alors \(F(b) = \int_a^b f(t) \, dt\).
Soit \(G\) une primitive quelconque de \(f\), alors \(G(x) = F(x) + k\) où \(k \in \mathbb{R}\).
Donc \(G(b) - G(a) = F(b) + k - F(a) - k = F(b) = \int_a^b f(t) \, dt\).
V. Tableau des primitives
Dans le tableau, \(u'\) est une fonction définie et continue sur l'intervalle \(I\).
| Fonction | Primitives | Définie sur |
| \(f(x) = a\) (constante) | \(F(x) = ax + k\) | \(\mathbb{R}\) |
| \(f(x) = x^n\) (\(n \in \mathbb{Z} \setminus \{-1\}\)) | \(F(x) = \frac{1}{n+1}x^{n+1} + k\) | \(\mathbb{R}\) si \(n \geq 0\) \(\mathbb{R}^*\) si \(n < 0\) |
| \(f(x) = \frac{1}{x}\) | \(F(x) = \ln|x| + k\) | \(]0; +\infty[\) |
| \(f(x) = e^x\) | \(F(x) = e^x + k\) | \(\mathbb{R}\) |
| \(f(x) = \cos x\) | \(F(x) = \sin x + k\) | \(\mathbb{R}\) |
| \(f(x) = \sin x\) | \(F(x) = -\cos x + k\) | \(\mathbb{R}\) |
| \(u' \cdot e^u\) | \(e^u + k\) | \(I\) |
| \(u' \cdot u^n\) (\(n \in \mathbb{Z} \setminus \{-1\}\)) | \(\frac{1}{n+1}u^{n+1} + k\) | \(I\) si \(n \geq 0\) \(I \cap \{x, u(x) \neq 0\}\) si \(n < 0\) |
| \(\frac{u'}{u}\) | \(\ln u + k\) | \(u(x) > 0\) sur \(I\) |
| \(\frac{u'}{u}\) | \(\ln(-u) + k\) | \(u(x) < 0\) sur \(I\) |
• \(f(x) = \frac{1}{x^2}\) sur \(\mathbb{R}^*\) → \(F(x) = -\frac{1}{x} + k\)
• \(f(x) = 2x \cdot e^{x^2-1}\) sur \(\mathbb{R}\) → \(F(x) = e^{x^2-1} + k\)
• \(f(x) = \frac{\ln x}{x}\) sur \(]0; +\infty[\) est de la forme \(u'u\) → \(F(x) = \frac{1}{2}(\ln x)^2 + k\)
VI. Intégration par parties
1. La formule
Soit \(u\) et \(v\) deux fonctions dérivables sur un intervalle \(I\) et \(a, b \in I\).
Alors \(\int_a^b u(x)v'(x) \, dx = [u(x)v(x)]_a^b - \int_a^b u'(x)v(x) \, dx\)
2. Démonstration
De la formule \((uv)' = u'v + uv'\), on tire \(uv' = (uv)' - u'v\).
En intégrant sur \([a; b]\) :
\(\int_a^b u(x)v'(x) \, dx = \int_a^b (uv)'(x) \, dx - \int_a^b u'(x)v(x) \, dx\)
\(= [u(x)v(x)]_a^b - \int_a^b u'(x)v(x) \, dx\)
3. Applications
On peut calculer des intégrales portant sur des fonctions dont on ne peut pas facilement déterminer une primitive. On peut aussi déterminer des primitives.
a) Déterminer \(\int_0^1 x \cdot e^x \, dx\)
b) Déterminer une primitive de \(\ln x\) sur \(]0; +\infty[\)
• Pour les fonctions de la forme \(P(x)e^x\) où \(P\) est un polynôme
• Pour les fonctions de la forme \(P(x)\ln x\) où \(P\) est un polynôme
VII. Calculs d'aires et de volumes
1. Calculs d'aires
Soit \(f\) et \(g\) deux fonctions continues sur \([a; b]\) telles que \(f(x) \leq g(x)\) sur \([a; b]\).
L'aire du domaine délimité par les courbes de \(f\) et \(g\) et les droites \(x = a\) et \(x = b\) est :
\(\mathcal{A} = \int_a^b [g(x) - f(x)] \, dx\)
Déterminer l'aire entre les courbes \(y = x^2\) et \(y = x^3\) sur \([0; 1]\).
• Points d'intersection : \(x^2 = x^3 \Leftrightarrow x = 0\) ou \(x = 1\)
• Sur \([0; 1]\), on a \(x^3 \leq x^2\)
• Aire = \(\int_0^1 (x^2 - x^3) \, dx = \frac{1}{12}\) u.a.
2. Calculs de volumes
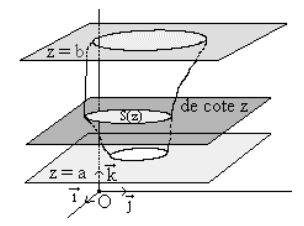
Soit un solide limité par les plans \(z = a\) et \(z = b\).
Si \(S(z)\) est l'aire de la section du solide par un plan perpendiculaire à l'axe \((Oz)\) en \(z\), alors :
\(\mathcal{V} = \int_a^b S(z) \, dz\)
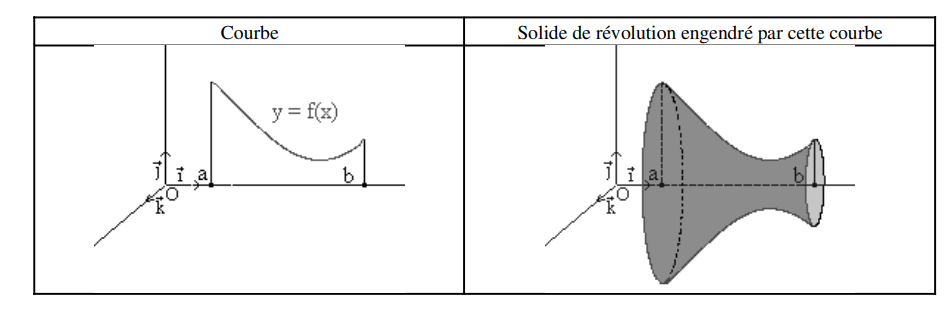
3. Volume d'un solide de révolution
Soit une région limitée par \(y = f(x)\), \(x = a\), \(x = b\) et l'axe \((Ox)\) tournant autour de l'axe \((Ox)\).
La section du solide par un plan perpendiculaire à \((Ox)\) est un disque de rayon \(|f(x)|\).
Le volume est : \(\mathcal{V} = \int_a^b \pi [f(x)]^2 \, dx\)
On considère le paraboloïde construit en faisant tourner la parabole \(y = x^2\) sur \([0; 1]\) autour de l'axe \((Oy)\).
Le paraboloïde est compris entre les plans \(y = 0\) et \(y = 1\).
La section par le plan perpendiculaire à \((Oy)\) est un disque de rayon \(x\), donc d'aire \(\pi x^2 = \pi y\).
Volume = \(\int_0^1 \pi y \, dy = \pi \left[\frac{y^2}{2}\right]_0^1 = \frac{\pi}{2}\) u.v.
Résumé
• Définition : L'intégrale \(\int_a^b f(t) \, dt\) représente l'aire sous la courbe de \(f\) sur \([a; b]\)
• Théorème fondamental : \(\int_a^b f(t) \, dt = F(b) - F(a)\) où \(F\) est une primitive de \(f\)
• Propriétés : Linéarité, relation de Chasles, inégalités
• Primitives : Table des primitives usuelles à connaître
• Intégration par parties : \(\int u v' = [uv] - \int u' v\)
• Applications : Calcul d'aires entre courbes et volumes de révolution
• Valeur moyenne : \(\mu = \frac{1}{b-a} \int_a^b f(t) \, dt\)
Exercices d'application
- Calculer \(\int_0^1 (3x^2 + 2x - 1) \, dx\)
- Déterminer une primitive de \(f(x) = \frac{2x+1}{x^2+x+1}\)
- Calculer \(\int_1^e x \ln x \, dx\) par intégration par parties
- Déterminer l'aire entre \(y = x^2\) et \(y = \sqrt{x}\) sur \([0; 1]\)
- Calculer le volume du solide engendré par la rotation de \(y = x^2\) autour de \((Ox)\) sur \([0; 2]\)
- Déterminer la valeur moyenne de \(f(x) = \sin x\) sur \([0; \pi]\)