Suites Et Reccurence
Terminale
COURS: Suites & Récurrences
Introduction
Les suites numériques sont des objets mathématiques fondamentaux qui permettent de modéliser de nombreux phénomènes évolutifs. Le raisonnement par récurrence est une méthode de démonstration puissante qui s'apparente à l'effet domino. Ce chapitre explore ces deux concepts essentiels en mathématiques.
I. Raisonnement par récurrence
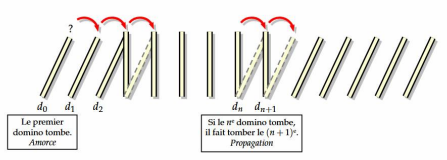
1. L'effet domino
Le raisonnement par récurrence fonctionne comme l'effet domino. Il faut deux conditions :
• L'amorce : Le premier domino d₀ tombe
• La propagation : Si un domino dₙ tombe, alors le suivant dₙ₊₁ tombe aussi
Soit la suite \((u_n)\) définie par \(u_0 = 0,3\) et \(\forall n \in \mathbb{N}, u_{n+1} = \frac{1}{2}u_n + \frac{1}{2}\)
Initialisation : \(u_0 = 0,3\) vérifie \(0 < u_0 < 1\) ✓
Hérédité : Si \(0 < u_n < 1\), alors \(0 < \frac{1}{2}u_n + \frac{1}{2} < 1\), donc \(0 < u_{n+1} < 1\) ✓
Conclusion : La propriété est vraie pour tout \(n \in \mathbb{N}\)
2. Conjecture et raisonnement par récurrence
- Calculer les premiers termes pour former une conjecture
- Démontrer l'hérédité de la propriété
- Vérifier l'initialisation pour un ou plusieurs rangs
- Conclure par le principe de récurrence
Soit \((u_n)\) définie par \(u_0 = 0\) et \(\forall n \in \mathbb{N}, u_{n+1} = 2u_n + 1\)
Conjecture : \(u_n = 2^n - 1\)
Hérédité : Si \(u_n = 2^n - 1\), alors \(u_{n+1} = 2(2^n - 1) + 1 = 2^{n+1} - 1\) ✓
Initialisation : \(u_0 = 0 = 2^0 - 1\) ✓
Conclusion : \(\forall n \in \mathbb{N}, u_n = 2^n - 1\)
3. Axiome de récurrence
Soit \(P_n\) une propriété définie sur \(\mathbb{N}\). Si :
• \(P_n\) est initialisée à partir du rang 0 (ou \(n_0\))
• \(P_n\) est héréditaire à partir du rang 0 (ou \(n_0\))
Alors \(P_n\) est vraie pour tout \(n \in \mathbb{N}\) à partir du rang 0 (ou \(n_0\))
Le raisonnement par récurrence comporte toujours deux phases :
- Prouver l'initialisation : la propriété est vraie au rang de départ
- Prouver l'hérédité : si la propriété est vraie au rang n, elle l'est au rang n+1
4. Inégalité de Bernoulli
Pour tout réel \(a > 0\) et pour tout \(n \in \mathbb{N}\) : \[(1 + a)^n \geq 1 + na\]
Initialisation : Pour \(n = 0\), \((1 + a)^0 = 1\) et \(1 + 0 \times a = 1\), donc \(1 \geq 1\) ✓
Hérédité : Supposons \((1 + a)^n \geq 1 + na\) (HR)
Alors \((1 + a)^{n+1} = (1 + a)^n \times (1 + a) \geq (1 + na)(1 + a) = 1 + na + a + na^2\)
Comme \(na^2 \geq 0\), on a \((1 + a)^{n+1} \geq 1 + (n+1)a\) ✓
5. Application aux suites
Soit \((u_n)\) définie par \(u_0 = 1\) et \(\forall n \in \mathbb{N}, u_{n+1} = \sqrt{2 + u_n}\)
Initialisation : \(u_0 = 1\) et \(u_1 = \sqrt{3} \approx 1,732\)
On a bien \(0 < 1 < \sqrt{3} < 2\) ✓
En ajoutant 2 : \(2 < 2 + u_n < 2 + u_{n+1} < 4\)
En prenant la racine : \(\sqrt{2} < u_{n+1} < u_{n+2} < 2\)
Comme \(\sqrt{2} \approx 1,414 > 0\), on a \(0 < u_{n+1} < u_{n+2} < 2\) ✓
6. Situations amenant à une conclusion erronée
Situation 1 : Hérédité seule vérifiée
Propriété : \(\forall n \in \mathbb{N}\), 3 divise \(2^n\)
Initialisation : 3 ne divise pas \(2^0 = 1\) ✗
Conclusion : La propriété est fausse malgré l'hérédité !
Propriété : \(\forall n \in \mathbb{N}\), \(n^2 - n + 41\) est premier
Contre-exemple : Pour \(n = 41\), on a \(41^2 - 41 + 41 = 41^2 = 1681 = 41 \times 41\)
Conclusion : La propriété est fausse ! L'initialisation seule ne suffit pas.
II. Limite d'une suite
1. Limite finie
On dit que la suite \((u_n)\) a pour limite \(\ell\) si, et seulement si, tout intervalle ouvert contenant \(\ell\) contient tous les termes de la suite à partir d'un certain rang.

Cette définition traduit l'accumulation des termes \(u_n\) autour de \(\ell\). Lorsque \(\ell\) existe, la limite est unique.
Les suites définies pour tout \(n \in \mathbb{N}^*\) par :
• \(\left(\frac{1}{\sqrt{n}}\right)\), \(\left(\frac{1}{n}\right)\), \(\left(\frac{1}{n^2}\right)\), ..., \(\left(\frac{1}{n^k}\right)\) avec \(k \in \mathbb{N}^*\)
ont pour limite 0
Déterminer à partir de quel entier n, le terme uₙ est dans un intervalle centré en l et de rayon 10⁻ᵖ.
Cette suite converge vers 0,5. Pour p = 3, on trouve n = 5.
from math import*
def lim(p):
u=0.1
n=0
while abs(u-0.5)>=10**(-p):
u=2u(1-u)
n+=1
return n
2. Limite infinie
On dit que la suite (uₙ) a pour limite +∞ (resp. -∞) si, et seulement si, tout intervalle ]A; +∞[ (resp. ]-∞; B[) contient tous les termes de la suite à partir d'un certain rang.
Pour une limite +∞, cette définition traduit l'idée que les termes de la suite arrivent à dépasser A, aussi grand soit-il. Une suite peut n'avoir aucune limite (ex: uₙ = (-2)ⁿ).
Les suites définies pour tout \(n \in \mathbb{N}\) par :
• \((\sqrt{n})\), \((n)\), \((n^2)\), ..., \((n^k)\) avec \(k \in \mathbb{N}^*\)
ont pour limite \(+\infty\)
Déterminer à partir de quel entier n, uₙ est supérieur à 10ᵖ.
Cette suite diverge vers \(+\infty\). Pour \(p = 3\), on trouve \(n = 25\).
def lim(p):
u=-2
n=0
while u<=10**p:
u=4/3*u+1
n+=1
return n
3. Limites par comparaison et par encadrement
Soit trois suites \((u_n)\), \((v_n)\), \((w_n)\). Si à partir de \(k \in \mathbb{N}\), on a :
• \(v_n \leq u_n \leq w_n\)
• \(\lim_{n \to +\infty} v_n = \ell\) et \(\lim_{n \to +\infty} w_n = \ell\)
Alors \(\lim_{n \to +\infty} u_n = \ell\)
Soit trois suites \((u_n)\), \((v_n)\), \((w_n)\). Si à partir de \(k \in \mathbb{N}\), on a :
• \(v_n \leq u_n \leq w_n\)
• \(\lim_{n \to +\infty} v_n = \ell\) et \(\lim_{n \to +\infty} w_n = \ell\)
• Si \(u_n \geq v_n\) et \(\lim_{n \to +\infty} v_n = +\infty\), alors \(\lim_{n \to +\infty} u_n = +\infty\)
• Si \(u_n \leq w_n\) et \(\lim_{n \to +\infty} w_n = -\infty\), alors \(\lim_{n \to +\infty} u_n = -\infty\)
Cas 1 : Si \(u_n \geq v_n\) et \(\lim_{n \to +\infty} v_n = +\infty\), alors \(\lim_{n \to +\infty} u_n = +\infty\)
Cas 2 : Si \(u_n \leq w_n\) et \(\lim_{n \to +\infty} w_n = -\infty\), alors \(\lim_{n \to +\infty} u_n = -\infty\)
Exemple 1 : \(u_n = \frac{\sin(n)}{n+1}\)
\(\forall n \in \mathbb{N}, -\frac{1}{n+1} \leq \frac{\sin(n)}{n+1} \leq \frac{1}{n+1}\)
Comme \(\lim_{n \to +\infty} \left(-\frac{1}{n+1}\right) = \lim_{n \to +\infty} \frac{1}{n+1} = 0\), on a \(\lim_{n \to +\infty} u_n = 0\)
\(\forall n \in \mathbb{N}, n + \sin(n) \geq n - 1\)
Comme \(\lim_{n \to +\infty} (n - 1) = +\infty\), on a \(\lim_{n \to +\infty} v_n = +\infty\)
4. Opérations sur les limites
4.1 Limite d'une somme
La limite d'une somme est généralement la somme des limites, sauf pour les formes indéterminées marquées F.I.
| Si (uₙ) a pour limite | l | l | +∞ | +∞ | +∞ | -∞ | -∞ |
| Si (vₙ) a pour limite | l' | +∞ | -∞ | +∞ | -∞ | +∞ | -∞ |
| alors (uₙ + vₙ) a pour limite | l + l' | +∞ | -∞ | +∞ | F.I.* | F.I.* | -∞ |
Exemple 1 : uₙ = 3n + 1 + 2/n
lim(3n + 1) = +∞ et lim(2/n) = 0, donc lim uₙ = +∞
lim((1/3)ⁿ) = 0 et lim(5 - 1/n) = 5, donc lim vₙ = 5
lim(n²) = +∞ et lim(-n + 2) = -∞ → Forme indéterminée
4.2 Limite d'un produit
La limite d'un produit est généralement le produit des limites, en appliquant la règle des signes pour les cas marqués ∞*.
| Si (uₙ) a pour limite | l | l ≠ 0 | 0 | ∞ | ∞ | ∞ |
| Si (vₙ) a pour limite | l' | ∞ | ∞ | ∞ | 0 | l' |
| alors (uₙ × vₙ) a pour limite | l × l' | ∞* | F.I. | ∞* | F.I. | ∞* |
Exemple 1 : wₙ = n² - n + 2 (résolution de la F.I.)
wₙ = n²(1 - 1/n + 2/n²)
lim(n²) = +∞ et lim(1 - 1/n + 2/n²) = 1, donc lim wₙ = +∞
lim(3ⁿ) = +∞ et lim(2 - n) = -∞, donc lim vₙ = -∞
4.3 Limite d'un quotient
La limite d'un quotient est généralement le quotient des limites, en appliquant la règle des signes pour les cas marqués ∞ ou 0.
| Si (uₙ) a pour limite | l | l ≠ 0 | 0 | l | ∞ | ∞ | ∞ |
| Si (vₙ) a pour limite | l' ≠ 0 | 0 | 0 | ∞ | l' | ∞ | ∞ |
| alors (uₙ/vₙ) a pour limite | l/l' | ∞* | F.I. | 0 | 0* | F.I. | ∞* |
(1) 0 signe constant : on écrira 0⁺ pour un nombre positif et 0⁻ pour un nombre négatif
Exemple 1 : uₙ = 5/(2n² + 1)
lim(5) = 5 et lim(2n² + 1) = +∞, donc lim uₙ = 0
lim(1 - n) = -∞ et lim(0,5ⁿ) = 0⁺, donc lim vₙ = -∞
wₙ = (n + 3/n)/(1 + 1/n)
lim(n + 3/n) = +∞ et lim(1 + 1/n) = 1, donc lim wₙ = +∞
5. Limite d'une suite géométrique
Soit q un réel. On a les limites suivantes :
• Si q > 1 alors lim qⁿ = +∞
• Si q = 1 alors lim qⁿ = 1
• Si -1 < q < 1 alors lim qⁿ = 0
• Si q ≤ -1 alors lim qⁿ n'existe pas
Soit q un réel. On a les limites suivantes :
• Si q > 1 alors lim qⁿ = +∞
• Si q = 1 alors lim qⁿ = 1
• Si -1 < q < 1 alors lim qⁿ = 0
• Si q ≤ -1 alors lim qⁿ n'existe pas
Posons q = 1 + a avec a > 0. D'après l'inégalité de Bernoulli :
qⁿ = (1 + a)ⁿ ≥ 1 + na
Comme lim(1 + na) = +∞, on a lim qⁿ = +∞
Étape 1 : Posons q = 1 + a avec a > 0 (car q > 1)
Étape 2 : D'après l'inégalité de Bernoulli :
(1 + a)ⁿ ≥ 1 + na pour tout n ∈ ℕ
Et que qⁿ = (1 + a)ⁿ ≥ 1 + na
Pour -1 < q < 1 et q ≠ 0, on pose Q = 1/|q| > 1. On utilise alors le cas précédent et la règle du quotient.
Soit (uₙ) définie par u₀ = 2 et uₙ₊₁ = 2uₙ + 5
Posons vₙ = uₙ + 5. Alors vₙ₊₁ = uₙ₊₁ + 5 = 2uₙ + 10 = 2(uₙ + 5) = 2vₙ
Donc (vₙ) est géométrique de raison q = 2 et de premier terme v₀ = 7
vₙ = 7 × 2ⁿ, donc uₙ = vₙ - 5 = 7 × 2ⁿ - 5
Comme 2 > 1, on a lim(2ⁿ) = +∞, donc lim uₙ = +∞
Définition : u₀ = 2 et uₙ₊₁ = 2uₙ + 5
Questions :
1) Montrer que la suite (vₙ) est géométrique
2) Exprimer vₙ puis uₙ en fonction de n
3) En déduire la limite de (uₙ)
1) Suite auxiliaire : Posons vₙ = uₙ + 5
vₙ₊₁ = uₙ₊₁ + 5 = (2uₙ + 5) + 5 = 2uₙ + 10 = 2(uₙ + 5) = 2vₙ
Donc (vₙ) est géométrique de raison q = 2 et v₀ = 7
3) Limite : Comme 2 > 1, lim(2ⁿ) = +∞, donc lim uₙ = +∞
6. Convergence d'une suite monotone
6.1 Suites majorées, minorées et bornées
Soit une suite (uₙ) :
• (uₙ) est majorée s'il existe M ∈ ℝ tel que : ∀n ∈ ℕ, uₙ ≤ M
• (uₙ) est minorée s'il existe m ∈ ℝ tel que : ∀n ∈ ℕ, uₙ ≥ m
• (uₙ) est bornée si elle est majorée et minorée
Soit une suite (uₙ) :
• (uₙ) est majorée s'il existe M ∈ ℝ tel que : ∀n ∈ ℕ, uₙ ≤ M
• (uₙ) est minorée s'il existe m ∈ ℝ tel que : ∀n ∈ ℕ, uₙ ≥ m
• (uₙ) est bornée si elle est majorée et minorée
Le majorant ou le minorant n'est pas unique. Si 2 majore la suite (uₙ), alors tout réel supérieur à 2 majore aussi (uₙ).
Montrer que uₙ = 1/(n+1) + 1/(n+2) + ... + 1/(2n) est bornée par [1/2; 1]
Minoration : uₙ ≥ 1/(2n) + 1/(2n) + ... + 1/(2n) = n × (1/(2n)) = 1/2
Conclusion : ∀n ∈ ℕ, 1/2 ≤ uₙ ≤ 1
Problème : Montrer que uₙ = 1/(n+1) + 1/(n+2) + ... + 1/(2n) est bornée par [1/2; 1]
Preuve de la majoration :
uₙ = 1/(n+1) + 1/(n+2) + ... + 1/(2n) (n termes)
≤ 1/n + 1/n + ... + 1/n (n termes)
= n × (1/n) = 1
Donc uₙ ≤ 1
uₙ = 1/(n+1) + 1/(n+2) + ... + 1/(2n) (n termes)
≥ 1/(2n) + 1/(2n) + ... + 1/(2n) (n termes)
= n × (1/(2n)) = 1/2
Donc uₙ ≥ 1/2
6.2 Théorèmes de divergence et de convergence
Soit (uₙ) une suite :
• Si (uₙ) est croissante et non majorée alors (uₙ) diverge vers +∞
• Si (uₙ) est décroissante et non minorée alors (uₙ) diverge vers -∞
Soit (uₙ) une suite :
• Si (uₙ) est croissante et non majorée alors (uₙ) diverge vers +∞
• Si (uₙ) est décroissante et non minorée alors (uₙ) diverge vers -∞
Soit (uₙ) croissante et non majorée. Pour tout intervalle ]A; +∞[, il existe N ∈ ℕ tel que uₙ ∈ ]A; +∞[.
Comme (uₙ) est croissante, ∀n > N, on a uₙ > uₙ, donc uₙ ∈ ]A; +∞[.
Donc à partir d'un certain rang, tous les termes sont dans ]A; +∞[. La suite diverge vers +∞.
Hypothèse : (uₙ) est croissante et non majorée
Étape 1 : (uₙ) n'est pas majorée, donc pour tout intervalle ]A; +∞[, il existe N ∈ ℕ tel que uₙ ∈ ]A; +∞[
Étape 2 : Comme (uₙ) est croissante, on a : ∀n > N, uₙ > uₙ
Étape 3 : Donc : ∀n > N, uₙ ∈ ]A; +∞[
Étape 4 : Donc à partir d'un certain rang, tous les termes de la suite sont dans l'intervalle ]A; +∞[
Conclusion : La suite (uₙ) diverge vers +∞
Soit (uₙ) définie par u₀ = 1 et uₙ₊₁ = uₙ + 2n + 3
Non majoration : Montrons par récurrence que ∀n ∈ ℕ, uₙ ≥ n²
• Initialisation : u₀ = 1 ≥ 0² ✓
• Hérédité : Si uₙ ≥ n², alors uₙ₊₁ = uₙ + 2n + 3 ≥ n² + 2n + 3 ≥ (n+1)² + 2 ≥ (n+1)² ✓
Donc (uₙ) n'est pas majorée
Définition : u₀ = 1 et uₙ₊₁ = uₙ + 2n + 3
1) Monotonie : ∀n ∈ ℕ, uₙ₊₁ - uₙ = 2n + 3 > 0, donc (uₙ) est croissante
2) Non majoration : Montrons par récurrence que ∀n ∈ ℕ, uₙ ≥ n²
• Initialisation : u₀ = 1 ≥ 0² ✓
• Hérédité : Si uₙ ≥ n², alors uₙ₊₁ = uₙ + 2n + 3 ≥ n² + 2n + 3 ≥ (n+1)² + 2 ≥ (n+1)² ✓
Donc (uₙ) n'est pas majorée
La réciproque est fausse ! Si une suite diverge vers +∞, elle n'est pas nécessairement croissante.
• Si une suite (uₙ) est croissante et majorée alors elle converge
• Si une suite (uₙ) est décroissante et minorée alors elle converge
• Si une suite (uₙ) est croissante et majorée alors elle converge
• Si une suite (uₙ) est décroissante et minorée alors elle converge
Soit (uₙ) définie par u₀ = 1 et uₙ₊₁ = √(2 + uₙ)
On a montré par récurrence que ∀n ∈ ℕ, 0 < uₙ < uₙ₊₁ < 2
Donc (uₙ) est croissante et majorée par 2, donc elle converge vers l avec 0 < l ≤ 2
Lorsqu'on passe à la limite, l'inégalité stricte uₙ < 2 devient large l ≤ 2.
On admet que la suite uₙ converge vers 2. Déterminer l'entier N à partir duquel uₙ > 1,999.
Résultat : lim(3) → 6, donc à partir de n ≥ 6, uₙ > 1,999
Problème : On admet que la suite uₙ converge vers 2. Déterminer l'entier N à partir duquel uₙ > 1,999.
Condition : uₙ > 1,999 ⇔ |uₙ - 2| < 10⁻³
Code Python :
Résultat : lim(3) → 6, donc à partir de n ≥ 6, uₙ > 1,999from math import*
def lim(p):
u=1
n=0
while abs(u-2)>=10**(-p):
u=sqrt(u+2)
n+=1
return n
7. Utilisation de la limite d'une suite
• Modélisation : Évolution de populations, croissance économique
• Algorithmes : Méthodes numériques, approximations
• Analyse : Continuité, dérivabilité, intégration
• Géométrie : Approximations de π, constructions géométriques
Résumé
• Le raisonnement par récurrence nécessite initialisation ET hérédité
• Les limites de suites peuvent être finies, infinies ou inexistantes
• Les opérations sur les limites suivent des règles précises (attention aux F.I.)
• Les suites géométriques ont des limites dépendant de leur raison
• Les suites monotones bornées convergent
• Les suites monotones non bornées divergent vers ±∞
• Les théorèmes de comparaison permettent de lever des indéterminations
Exercices d'application
- Démontrer par récurrence que ∀n ∈ ℕ, 1 + 2 + ... + n = n(n+1)/2
- Calculer les limites des suites : uₙ = (2n+1)/(n-3), vₙ = n² - 3n + 1
- Étudier la convergence de la suite définie par u₀ = 1 et uₙ₊₁ = (uₙ + 2)/3
- Démontrer que la suite uₙ = 1 + 1/2 + ... + 1/n diverge vers +∞
- Calculer lim(n→∞) (1 + 1/n)ⁿ
- Étudier la suite géométrique de premier terme 5 et de raison 0,8